锯齿状张量运算符

高层概述

锯齿状张量运算符的目的是处理输入数据的某个维度是“锯齿状”的情况，即给定维度中的每个连续行可能具有不同的长度。这类似于 PyTorch 中的 NestedTensor 实现 和 TensorFlow 中的 RaggedTensor 实现。

这种输入类型的两个显著示例是

• 推荐系统中的稀疏特征输入

• 可能作为自然语言处理系统输入的标记化句子批次。

锯齿状张量格式

在 FBGEMm_GPU 中，锯齿状张量有效地表示为三张量对象。这三个张量是：**值**、**最大长度**和**偏移**。

值

Values 定义为一个二维张量，其中包含锯齿状张量中的所有元素值，即 Values.numel() 是锯齿状张量中的元素数量。 Values 中每行的尺寸派生自锯齿状张量中最小（最内层）维度子张量（不包括大小为 0 的张量）的最大公约数。

偏移

Offsets 是一个张量列表，其中每个张量 Offsets[i] 代表列表中下一个张量 Offsets[i + 1] 的值的分区索引。

例如，Offset[i] = [ 0, 3, 4 ] 意味着当前维度 i 被划分为两个组，由索引边界 [0 , 3) 和 [3, 4) 表示。对于每个 Offsets[i]，其中 0 <= i < len(Offests) - 1，Offsets[i][0] = 0，并且 Offsets[i][-1] = Offsets[i+1].length。

Offsets[-1] 指的是 Values 的外层维度索引（行索引），即 offsets[-1] 将是 Values 本身的分区索引。因此，Offsets[-1]，张量以 0 开始，以 Values.size(0)（即 Values 的行数）结束。

最大长度

MaxLengths 是一个整数列表，其中每个值 MaxLengths[i] 代表 Offsets[i] 中相应偏移值之间的最大值。

MaxLengths[i] = max( Offsets[i][j] - Offsets[i][j-1]  |  0 < j  < len(Offsets[i]) )

MaxLengths 中的信息用于执行从锯齿状张量到普通（密集）张量的转换，它将用于确定张量密集形式的形状。

锯齿状张量示例

下图显示了一个包含三个二维子张量的锯齿状张量示例，每个子张量具有不同的维度。

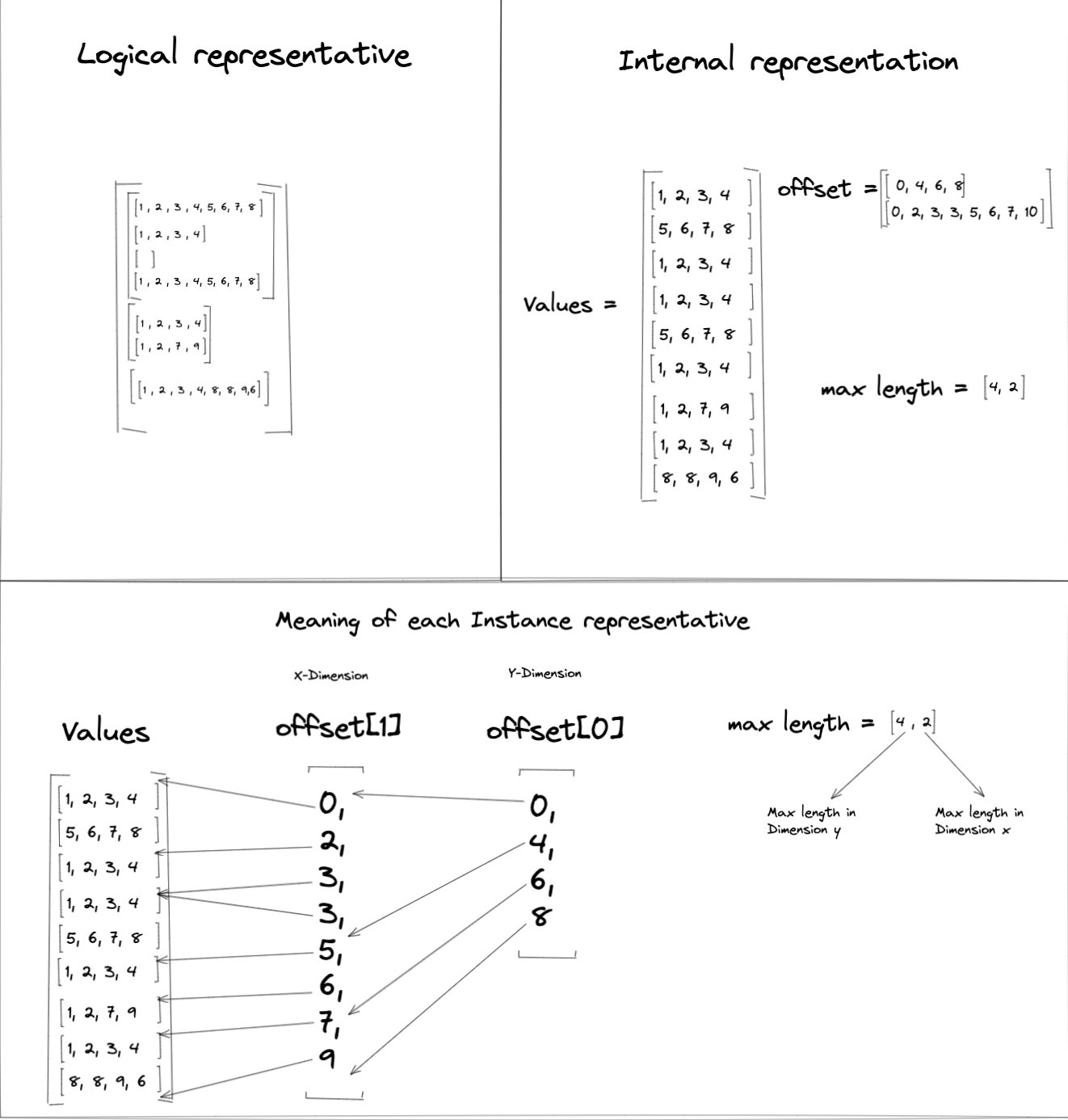
在此示例中，锯齿状张量最内层维度的行大小分别为 8、4 和 0，因此 Values 中每行的元素数量设置为 4（最大公约数）。这意味着 Values 的大小必须为 9 x 4 才能容纳锯齿状张量中的所有值。

由于示例锯齿状张量包含二维子张量，因此 Offsets 列表的长度需要为 2，以创建分区索引。 Offsets[0] 代表维度 0 的分区，Offsets[1] 代表维度 1 的分区。

示例锯齿状张量中的 MaxLengths 值为 [4 , 2]。 MaxLengths[0] 源自 Offsets[0] 范围 [4, 0)，而 MaxLengths[1] 源自 Offsets[1] 范围 [0, 2)（或 [7, 9]，[3,5]）。

下表展示了应用于 Values 张量的分区索引，用于构造示例锯齿状张量的逻辑表示。

Offsets[0]	Offsets[0] 范围	Offsets[0] 组	对应的 Offsets[1]	Offsets[1] 范围	Values 组	对应的 Values
[ 0, 4, 6, 8 ]	[0, 4)	第 1 组	[ 0, 2, 3, 3, 5 ]	[ 0, 2 )	第 1 组	[ [ 1, 2, 3, 4 ], [ 5, 6, 7, 8 ] ]
				[ 2, 3 )	第 2 组	[ [ 1, 2, 3, 4 ] ]
				[ 3, 3 )	第 3 组	[ ]
				[ 3, 5 )	第 4 组	[ [ 1, 2, 3, 4 ], [ 5, 6, 7, 8 ] ]
	[4, 6)	第 2 组	[ 5, 6, 7 ]	[ 5, 6 )	第 5 组	[ [ 1, 2, 3, 4 ] ]
				[ 6, 7 )	第 6 组	[ [ 1, 2, 7, 9 ] ]
	[6, 8)	第 3 组	[ 7, 9 ]	[ 7, 9 )	第 7 组	[ [ 1, 2, 3, 4 ], [ 8, 8, 9, 6 ] ]

锯齿状张量操作

目前，FBGEMM_GPU 只支持锯齿状张量的逐元素加法、乘法和转换操作。

算术运算

锯齿状张量的加法和乘法类似于 Hadamard 乘积，并且仅涉及锯齿状张量的 Values。例如：

\[\begin{split}\begin{bmatrix} \begin{bmatrix} 1. & 2. \\ 3. & 4. \\ \end{bmatrix} \\ \begin{bmatrix} 5. & 6. \\ \end{bmatrix} \\ \begin{bmatrix} 7. & 8. \\ 9. & 10. \\ 11. & 12. \\ \end{bmatrix} \\ \end{bmatrix} \times \begin{bmatrix} \begin{bmatrix} 1. & 2. \\ 3. & 4. \\ \end{bmatrix} \\ \begin{bmatrix} 5. & 6. \\ \end{bmatrix} \\ \begin{bmatrix} 7. & 8. \\ 9. & 5. \\ 2. & 3. \\ \end{bmatrix} \\ \end{bmatrix} \rightarrow \begin{bmatrix} \begin{bmatrix} 1. & 4. \\ 9. & 16. \\ \end{bmatrix} \\ \begin{bmatrix} 25. & 36. \\ \end{bmatrix} \\ \begin{bmatrix} 49. & 64. \\ 81. & 50. \\ 22. & 36. \\ \end{bmatrix} \\ \end{bmatrix}\end{split}\]

因此，锯齿状张量上的算术运算要求两个操作数具有相同的形状。换句话说，如果我们有锯齿状张量 \(A\)、\(X\)、\(B\) 和 \(C\)，其中 \(C = AX + B\)，则以下属性成立：

// MaxLengths are the same
C.maxlengths == A.maxlengths == X.maxlengths == B.maxlengths

// Offsets are the same
C.offsets == A.offsets == X.offsets == B.offsets

// Values are elementwise equal to the operations applied
C.values[i][j] == A.values[i][j] * X.values[i][j] + B.values[i][j]

转换操作

锯齿状到密集

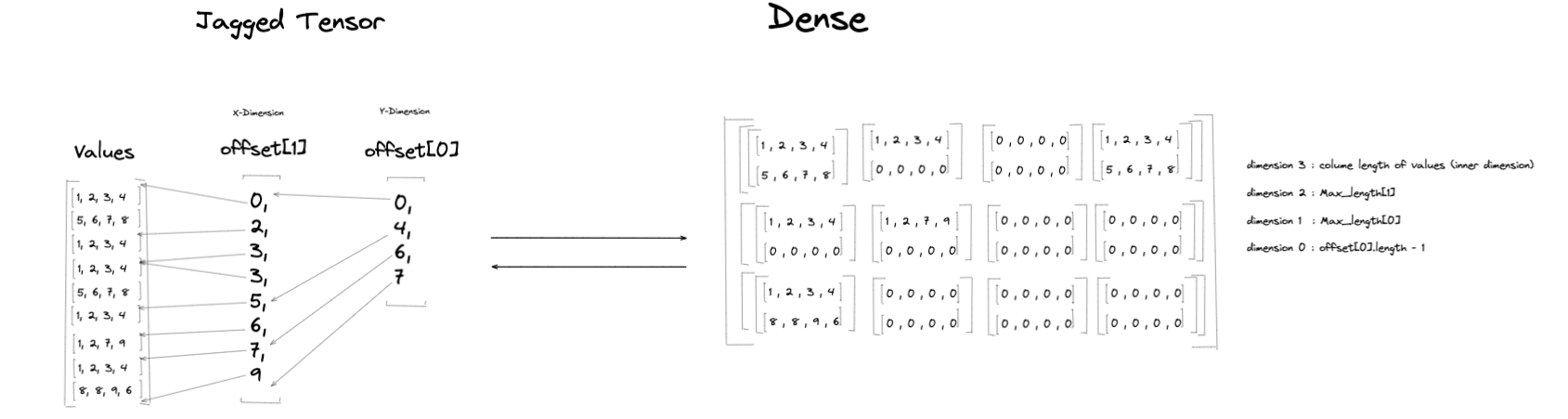
将锯齿状张量 \(J\) 转换为等效的密集张量 \(D\) 从一个空的密集张量开始。 \(D\) 的形状基于 MaxLengths、Values 的内层维度以及 Offsets[0] 的长度。 \(D\) 的维度数量为：

rank(D) = len(MaxLengths) + 2

对于 \(D\) 的每个维度，其维度大小为：

dim(i) = MaxLengths[i-1]  // (0 < i < D.rank-1)

使用 锯齿状张量示例 中的示例锯齿状张量，len(MaxLengths) = 2，因此等效密集张量的秩（维度数量）将为 4。该示例锯齿状张量有两个偏移张量，Offsets[0] 和 Offsets[1]。在转换过程中，来自 Values 的元素将根据 Offsets[0] 和 Offsets[1] 的分区索引中表示的范围加载到密集张量中（请参阅 表格 以获取组到密集表格相应行的映射）。

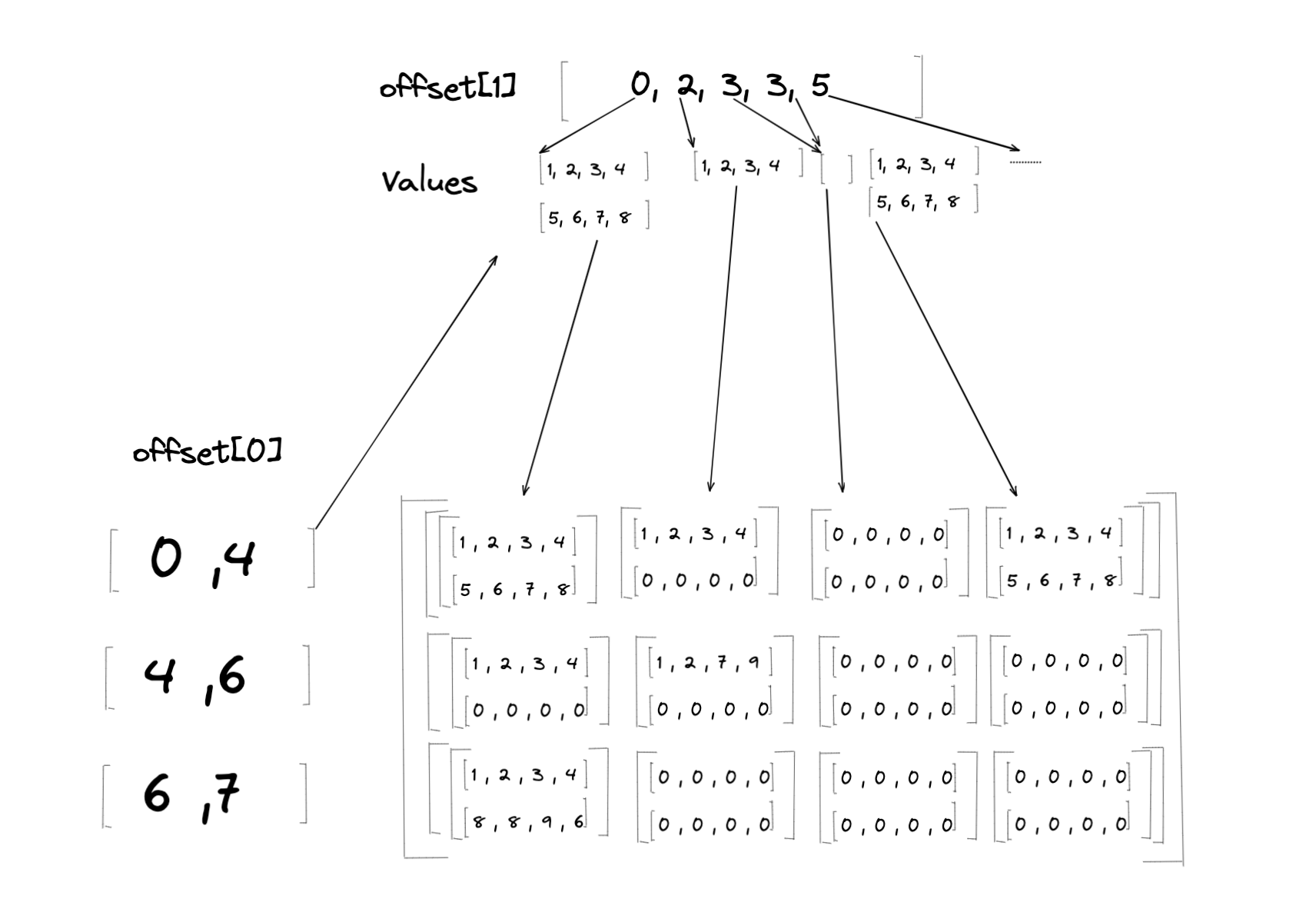
\(D\) 的某些部分将不会加载 \(J\) 的值，因为 Offsets[i] 中表示的每个分区范围的大小都不等于 MaxLengths[i]。在这种情况下，这些部分将被填充值填充。在上面的示例中，填充值为 0。

密集到锯齿状

对于从密集到锯齿状张量的转换，密集张量中的值将被加载到锯齿状张量的 Values 中。但是，给定密集张量可能与 Offsets 引用的形状不符。这可能导致锯齿状张量无法读取相应的密集位置，如果密集的相关维度小于预期。发生这种情况时，我们将向相应的 Values 提供填充值（如下所示）。

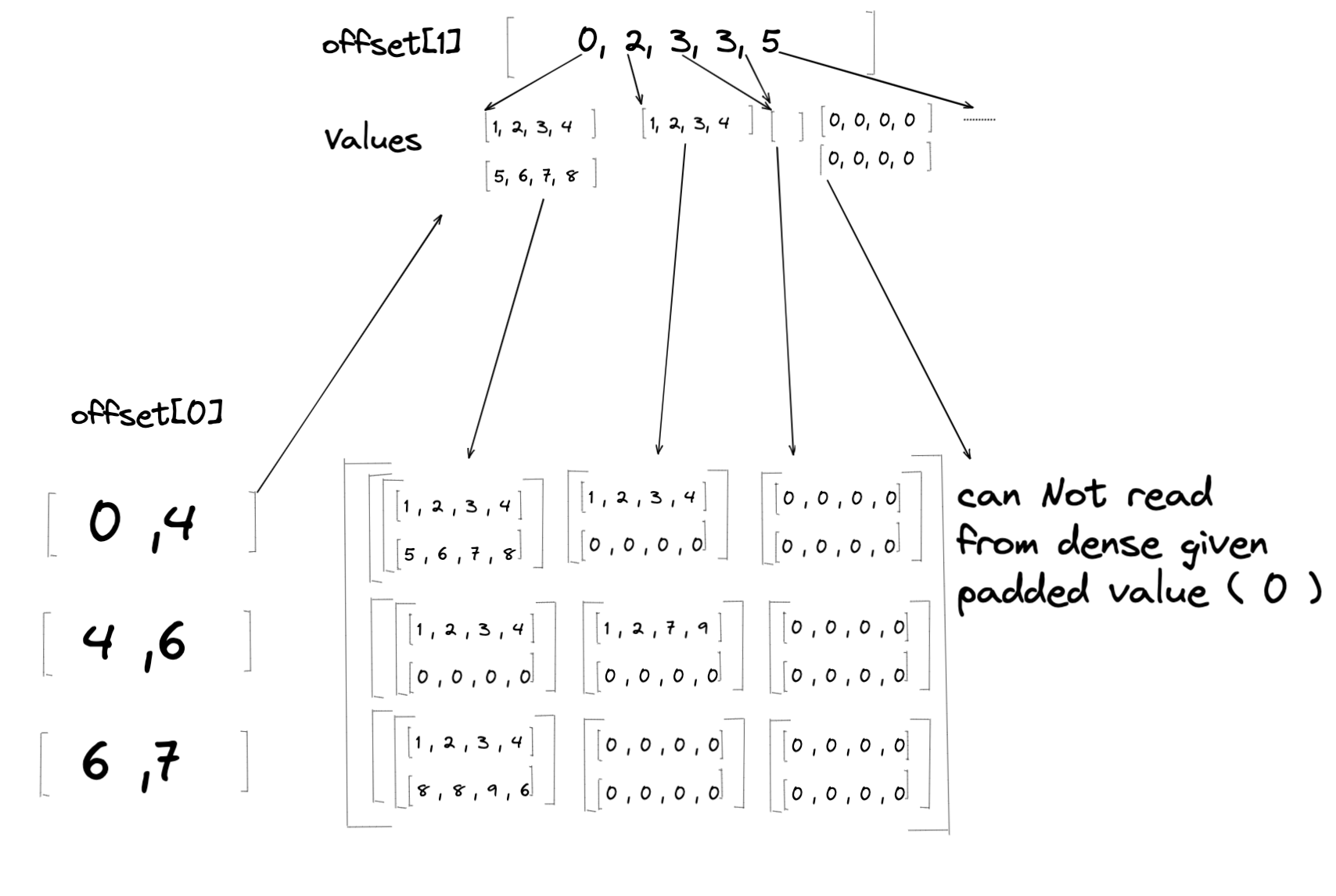
组合算术 + 转换操作

在某些情况下，我们希望执行以下操作：

dense_tensor + jagged_tensor → dense_tensor (or jagged_tensor)

我们可以将此类操作分解为两个步骤：

1. 转换操作 - 根据目标张量所需的格式，从锯齿状到密集或从密集到锯齿状进行转换。转换后，操作数张量（无论是密集还是锯齿状）应具有完全相同的形状。

2. 算术运算 - 照常对密集或锯齿状张量执行算术运算。