稀疏性概述¶
稀疏性是一种从神经网络中移除参数的技术,以降低其内存开销或延迟。通过仔细选择剪枝元素的方式,可以在不显著牺牲模型质量(准确率/f1值)的情况下,显著降低内存开销和延迟。
目标¶
我们认为当前稀疏性研究人员/用户面临的主要问题是碎片化。研究人员理应展示端到端的成果,但这却意味着他们需要花费大量时间来弄清楚如何与 PyTorch 集成,以及实现上的问题,例如:
何时应该进行掩码处理?
何时/如何存储压缩表示?
是否需要原地或非原地掩码更新?
如何调用稀疏矩阵乘法而不是密集矩阵乘法?
我们认为上述问题可以通过 torchao 一次性解决,让研究人员专注于真正重要的事情——提升稀疏核性能或更精确的剪枝算法。
更具体地说,我们希望为稀疏核(张量子类)和剪枝算法(torch.ao.pruning.Sparsifier)提供用户可以扩展的教程和 API。我们的目标是提供模块化的构建块,不仅可以用于加速推理,还可以用于训练,并且可以很好地与 torchao 量化工作流结合使用。
从头开始训练稀疏模型,并实现硬件加速,同时将准确率损失降至最低。
使用自定义剪枝算法恢复剪枝模型的准确率损失。
在支持稀疏性的硬件上加速掩码/剪枝模型,以实现性能提升。
设计¶
稀疏性与量化一样,是一种准确率/性能的权衡,我们不仅关心加速效果,还关心架构优化技术的准确率下降情况。
在量化中,理论性能增益通常由我们量化到的数据类型决定——从 float32 量化到 float16 会带来理论上的 2 倍加速。对于剪枝/稀疏性,类似的变量将是稀疏级别/稀疏模式。对于半结构化稀疏性,稀疏级别固定为 50%,因此我们期望理论上能有 2 倍的提升。对于块稀疏矩阵和非结构化稀疏性,加速效果是可变的,取决于张量的稀疏级别。
稀疏性和量化之间的一个关键区别在于准确率下降的确定方式:通常,量化的准确率下降由所选的 scale 和 zero_point 决定。然而,在剪枝中,准确率下降取决于掩码。稀疏性和量化密切相关,并且共享量化/稀疏感知训练等准确率缓解技术。
通过仔细选择指定的元素并重新训练网络,剪枝可以实现可忽略的准确率下降,甚至在某些情况下可以略微提高准确率。这是一个活跃的研究领域,目前尚未达成一致意见。我们期望用户会根据自己设定的目标稀疏模式进行剪枝。
给定目标稀疏模式,剪枝/稀疏化模型可以被视为两个独立的问题:
准确率 - 如何找到一组满足目标稀疏模式的稀疏权重,以最小化模型的准确率下降?
性能 - 如何加速稀疏权重以进行推理并减少内存开销?
我们的工作流设计为两个部分,分别独立地回答这两个问题:
一个前端 Python 用户界面 API,用于为任何任意稀疏模式查找稀疏权重。
一个后端稀疏核/操作集合,用于减少内存/延迟。
这两部分之间的交接点是将稀疏权重以密集格式存储,并将缺失元素的位置填充为 0。这是一个自然的交接点,因为稀疏矩阵乘法和使用该张量的密集矩阵乘法在数值上是等价的。这使我们能够为用户提供清晰的后端接口,针对给定的稀疏模式:
如果您能将您的密集矩阵转换为 **2:4 稀疏格式**,我们可以在没有数值损失的情况下,将矩阵乘法速度提高 **1.7 倍**。
这还允许用户利用我们快速的稀疏核,即使他们现有的稀疏权重已经是密集格式。我们预计许多用户会提出自己定制的前端掩码解决方案,或者使用其他第三方解决方案,因为这是一个活跃的研究领域。
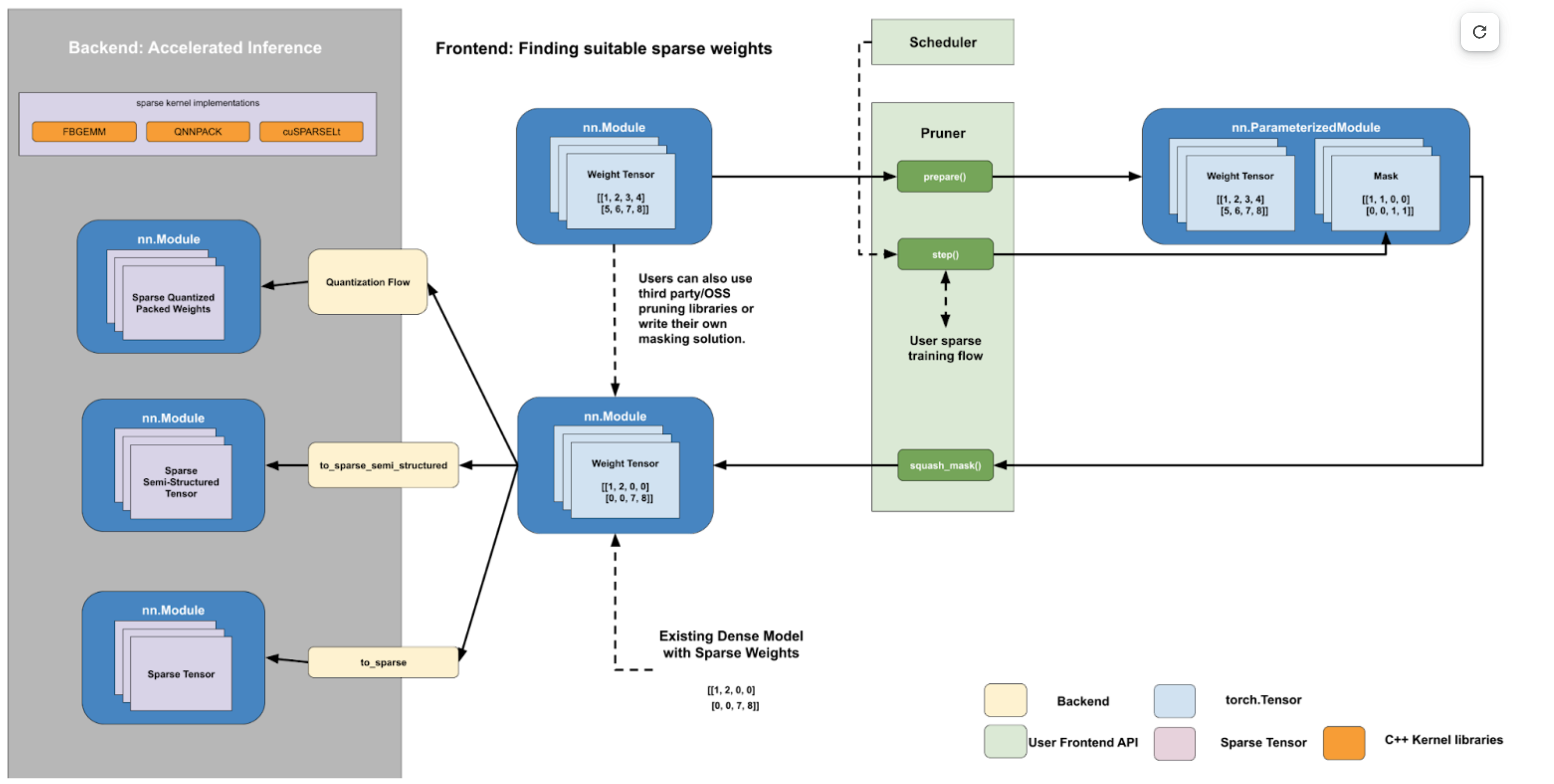
下面,我们提供一个使用我们的 PyTorch API 加速具有 2:4 稀疏性和 bf16 的模型的示例。
import torch
from torch.sparse import to_sparse_semi_structured, SparseSemiStructuredTensor
from torch.ao.pruning import WeightNormSparsifier
# bfloat16 CUDA model
model = model.half().cuda()
# Accuracy: Finding a sparse subnetwork
sparse_config = []
for name, mod in model.named_modules():
if isinstance(mod, torch.nn.Linear):
sparse_config.append({"tensor_fqn": f"{name}.weight"})
sparsifier = WeightNormSparsifier(sparsity_level=1.0,
sparse_block_shape=(1,4),
zeros_per_block=2)
# attach FakeSparsity
sparsifier.prepare(model, sparse_config)
sparsifier.step()
sparsifier.squash_mask()
# now we have dense model with sparse weights
# Performance: Accelerated sparse inference
for name, mod in model.named_modules():
if isinstance(mod, torch.nn.Linear):
mod.weight = torch.nn.Parameter(to_sparse_semi_structured(mod.weight))
从根本上说,流程是通过操作 torch.Tensors 来实现的。在前端,我们在 sparse_config 字典中通过张量的完全限定名称指定张量。前端设计遵循量化 API,有一个 prepare 函数,它将 FakeSparsity 参数化附加到 config 中指定的张量上。
FakeSparsity 是一种参数化,它模拟非结构化稀疏性,其中每个元素都有一个掩码。因此,我们可以使用它来模拟我们想要的任何稀疏模式。
用户将使用自己的自定义代码训练准备好的模型,并在必要时调用 .step() 来更新掩码。一旦他们找到合适的掩码,他们将调用 squash_mask() 将掩码融合到权重中,创建一个在正确位置带有 0 的密集张量。
用户随后将通过使用量化流程进行量化块稀疏 CPU 推理,或者调用指定权重张量上的 to_sparse_semi_structured 来转换他们的模型以进行加速稀疏推理。
背景¶
本节将介绍神经网络剪枝/稀疏性的一些背景知识,以及一些常见剪枝/稀疏性术语的定义。在学术界/工业界,**剪枝**和**稀疏性**经常被互换使用,指代同一件事。这可能会造成混淆,尤其是因为稀疏性是一个被过度使用的术语,它可以指代许多其他事物,例如稀疏张量表示。
请注意,本节侧重于**剪枝**,而不是**稀疏训练**。区别在于,在**剪枝**中,我们从一个预训练的密集模型开始,而在**稀疏训练**中,我们从头开始训练一个稀疏模型。
为避免混淆,我们通常尝试使用稀疏性来指代张量。请注意,稀疏张量可以指代包含许多零值的密集张量,或者使用稀疏表示存储的张量。我们将该流程描述为**剪枝**,将产生的模型描述为**剪枝模型**。
大体上,实现更优化的剪枝模型的流程如下:

剪枝的总体思想是,我们可以掩盖掉一个已训练神经网络的某些权重,并恢复任何准确率损失。由此产生的剪枝模型可以在利用这种稀疏性的优化核上运行,以实现加速推理。
默认情况下,将剪枝参数归零不会影响模型的延迟/内存开销。这是因为密集张量本身仍然包含剪枝的元素(零值元素),并且在矩阵乘法期间仍会使用这些元素进行计算。为了实现性能提升,我们需要将我们的密集核替换为稀疏核。
广义来说,这些稀疏表示允许我们跳过涉及剪枝元素的计算,以加速矩阵乘法。为此,这些优化的稀疏核在存储格式更高效的稀疏矩阵上工作。一些稀疏张量布局与特定后端(如 NVIDIA 2:4)紧密耦合,而另一些则更通用,并被多个后端支持(CSC 被 FBGEMM 和 QNNPACK 支持)。
| 名称 | 描述 | 稀疏矩阵的存储方式 |
| COO (sparse_coo) | COOrdinate (坐标) 格式用于存储稀疏矩阵。矩阵存储为非稀疏数据向量和这些元素在密集矩阵中的索引位置的组合。 | 稀疏矩阵 = {索引:坐标位置张量,数据:对应于索引位置的值张量} |
| BSR (sparse_bsr) | 块稀疏行 (Block sparse row) 格式用于存储稀疏矩阵。矩阵存储为数据块,以及这些块在密集矩阵中的索引位置。与 COO 非常相似,不同之处在于单个数据由块而不是标量组成。 | 稀疏矩阵 = {索引:坐标位置张量,二维用于矩阵,数据:对应于索引位置的块张量},其中块是对应于稀疏模式的矩阵。 |
| CSR (sparse_csr) / CSC (sparse_csc) | 压缩稀疏行/列 (Compressed sparse row/column) 格式用于存储稀疏矩阵。稀疏矩阵存储为列/行上的数据块,以及这些行/列在密集矩阵中的索引。这是存储块稀疏矩阵最紧凑的格式。 | 稀疏矩阵 = {索引:一维列索引张量,IndexPtr:一维张量,指定行对应的列的开始和结束索引,从行 0 开始,数据:对应于索引位置的块张量。} |
| NVIDIA 2:4 压缩表示 | 自定义 NVIDIA 压缩存储格式,用于 2:4 半结构化稀疏性。我们将稀疏矩阵存储为压缩的密集矩阵(尺寸减半),其中包含非剪枝元素和一个位掩码索引。当我们将稀疏矩阵乘以另一个密集矩阵时,我们使用掩码来索引密集矩阵并与我们的压缩密集矩阵相乘。 | 稀疏矩阵 = {位掩码:剪枝元素的 2 位索引,压缩密集矩阵:包含所有非剪枝元素,尺寸是原始密集矩阵的一半} |
表 4.1:常见稀疏张量布局概述。
虽然剪枝的总体思想很简单,但在成功剪枝模型之前,用户需要弄清楚许多细节。
这些可以大致分为以下几类:
剪枝配置 - 我应该剪枝哪些层?我应该剪枝到什么稀疏级别?
剪枝标准 - 我应该如何决定移除哪些参数?
剪枝策略 - 一旦我移除了参数,我该如何恢复准确率损失?
稀疏模式 - 我在剪枝模型时应该尝试使用特定的稀疏模式吗?不同的硬件后端支持不同稀疏模式的加速推理。
剪枝配置¶
神经网络中的所有层并非都一样。有些层对剪枝可能比其他层更敏感。用户必须决定要剪枝哪些层,以及每个层的**稀疏级别**,即该权重张量的零值百分比。剪枝配置对剪枝模型的准确率和加速效果都有影响。
确定给定模型的最佳剪枝配置和稀疏级别是一个开放性问题,不存在通用解决方案。这部分是因为最优剪枝配置依赖于后续的剪枝标准和策略,并且存在无数种决定如何剪枝模型以及如何恢复丢失准确率的方法。
确定要剪枝的层及其程度的一种常用方法是执行敏感性分析,方法是:在不同稀疏级别下剪枝模型中的每个层,并查看随后的准确率下降(无需重新训练)。这为用户提供了每个层的稀疏度-准确率曲线,用户随后可以使用该曲线作为代理来确定最佳剪枝配置。
剪枝标准¶
用户必须决定从神经网络中移除参数的标准。与确定最佳剪枝配置类似,确定最佳剪枝标准是一个开放的研究问题,并且依赖于上述其他因素。
最常见的剪枝标准是使用权重幅度。其思想是,低幅度权重对模型输出的贡献小于高幅度权重。如果我们想移除参数,我们可以移除绝对值最小的权重。
然而,即使使用简单的剪枝标准(如权重幅度),用户也需要考虑其他因素:
局部 vs. 全局范围
局部范围意味着掩码仅根据层统计信息进行计算。
优点:掩码计算简单。
缺点:准确率与稀疏度权衡可能不是最优的。
全局范围意味着稀疏统计信息不受单个层限制,但如果需要,可以跨越多个层。
优点:无需设置每层阈值。张量统计信息在层之间共享,并使用层间归一化来实现。
缺点:计算掩码时复杂度增加。
用于掩码计算的张量
权重:仅使用权重张量来计算掩码。此方法对推理来说最简单,因为权重张量是恒定的。
梯度:基于权重和梯度范数计算重要性。常用于预训练方法。目前 CTR_mobile_feed 使用基于梯度的剪枝算法。
激活:在一些研究论文中,与目标权重相对应的激活的范数被用于计算重要性得分。
原地或非原地掩码更新
原地更新通过执行 W = W * (Mask) 来更新稀疏张量。一旦权重张量被更新,稀疏值将被归零,无法恢复。
优点:只需要存储稀疏张量的一个副本(+掩码)。
缺点:一旦掩码应用于权重,权重就会被归零,所有过去的历史都将丢失。这些权重无法再生。
非原地更新不直接修改张量,而是执行以下操作:W' = W * (Mask) and dW' = dW * (Mask)。
优点:原始张量得以保留(掩码元素不通过反向传播更新)。如果掩码发生变化,权重可以再生。这对于 PAT 是必需的。
缺点:除了未掩码的权重 (W) 外,还会计算掩码的权重 (W'),并在内存中保留用于前向/后向计算。
| 名称 | 描述 | 注意事项 |
| 幅度 / 重要性 | 移除范数最小的参数(通常使用 L1)。 | 已被证明在 2:4 半结构化稀疏性下效果良好。通过在一次性幅度剪枝后重复训练循环,可以实现与原始模型相同的准确率。 |
| 移动剪枝 | 这些方法旨在利用梯度信息来决定移除哪些参数。其思想是移除在微调过程中变化不大的参数。 | 常用于预训练模型。 |
| 低秩分解 | 这些方法旨在用 SQx 替换 Wx,其中 S 和 Q 是低秩矩阵。 | 通常,这些方法使用某种层级重建,即不通过训练模型来恢复丢失的准确率,而是寻求匹配层级统计信息(找到 SQx,使得 L2(SQx, Wx) 最小化)。 |
| 随机 | 随机移除参数。 |
表 4.2:一些常见剪枝标准的描述。
剪枝策略¶
这是一个通用术语,描述了用户尝试恢复其剪枝模型的准确率下降的方法。在剪枝模型后,通常会看到模型的准确率下降,因此用户通常会重新训练剪枝模型以进行纠正。剪枝策略还决定了在模型训练期间何时以及多久进行一次剪枝。
剪枝策略和剪枝标准之间的界限并不明确,尤其是在剪枝感知训练方法的情况下,这些方法会在训练期间更新掩码。我们有时使用**剪枝** **算法**这个术语来指代这两项的组合。这两个因素以及剪枝配置最终决定了剪枝模型的最终准确率。
| 剪枝策略 | 描述 | 注意事项 |
| 零次迭代 | 剪枝一次,不重新训练模型。 | 这些方法依赖于更复杂的剪枝标准。 这在文献中有时被称为一次性剪枝,但我们将一次性剪枝定义为剪枝一次并重新训练一次。 |
| 一次性 | 剪枝一次,重新训练模型一次。 | NVIDIA 已证明,一次性 2:4 半结构化稀疏剪枝在各种常见的视觉/NLP 模型上都能很好地泛化。 \ \ 重训练策略是简单地再次重复训练过程。 |
| 迭代 | 剪枝模型,重新训练,重复。 | 我们可以迭代地增加稀疏级别,或迭代地剪枝模型中的不同层。 |
| 剪枝感知训练 | 在训练期间学习掩码。 | CTR_feed 目前的剪枝算法使用的就是此方法。 |
| NAS / 多掩码 | 训练期间使用多个掩码。这可以被视为一种神经架构搜索。 | PySpeech (FastNAS) 使用。 |
| 层级重建 | 与使用损失函数进行重新训练不同,我们试图通过使用类似于知识蒸馏的双模型方法来尽可能多地从每个层恢复信息。 | 参见 https://arxiv.org/pdf/2204.09656.pdf |
表 4.3:一些常见剪枝策略的描述。
稀疏模式¶
稀疏模式描述了剪枝的参数在模型/张量内的排列方式。
请记住,通常需要使用优化的稀疏核才能实现性能提升。根据权重张量的格式和稀疏级别,稀疏矩阵乘法可能比其密集对应项更快。如果张量不够稀疏,它也可能更慢。
在最普遍的层面上,剪枝是非结构化的——每个参数都有自己的掩码。这提供了最大的灵活性,但需要非常高的稀疏度(>98%)才能提供性能优势。为了在较低的稀疏级别提供加速推理,硬件后端增加了对特殊稀疏模式的支持。
我们寻求以模型剪枝的方式,使权重张量呈现与我们的推理后端相同的稀疏模式。如果我们能够恢复丢失的准确率,同时保持稀疏模式,我们就可以在稀疏硬件上以加速推理的方式运行该模型,而不会有准确率损失。我们也可以在目标后端上运行以不同稀疏模式剪枝的模型,但会牺牲一些额外的准确率损失。
具体的后端硬件及其对应的稀疏模式,以及剪枝配置,最终决定了我们观察到的性能加速效果。如果我们使用不同的剪枝标准来剪枝模型,如果它遵循相同的稀疏模式和稀疏级别,它将具有相同的性能特征。例如,如果我们决定移除幅度最高的权重而不是幅度最低的权重,我们预计这不会改变剪枝模型的性能特征。
| 稀疏模式 | 掩码可视化
(50% 稀疏级别) |
||||||||||||||||||||||||||||||||
| 非结构化稀疏性 |
|
||||||||||||||||||||||||||||||||
| 2:4 半结构化 |
|
||||||||||||||||||||||||||||||||
| 块稀疏性 |
|
||||||||||||||||||||||||||||||||
| 结构化稀疏性 |
|
表 4.4:一些常见稀疏模式的描述。
有关我们支持的 API 和基准测试的更多信息,请参阅 稀疏性 README。
