注意
点击 此处 下载完整的示例代码
音频重采样¶
作者: Caroline Chen, Moto Hira
本教程展示了如何使用 torchaudio 的重采样 API。
import torch
import torchaudio
import torchaudio.functional as F
import torchaudio.transforms as T
print(torch.__version__)
print(torchaudio.__version__)
2.10.0.dev20251013+cu126
2.8.0a0+1d65bbe
准备¶
首先,我们导入模块并定义辅助函数。
import math
import timeit
import matplotlib.pyplot as plt
from IPython.display import Audio
import numpy as np
DEFAULT_OFFSET = 201
def _get_log_freq(sample_rate, max_sweep_rate, offset):
"""Get freqs evenly spaced out in log-scale, between [0, max_sweep_rate // 2]
offset is used to avoid negative infinity `log(offset + x)`.
"""
start, stop = math.log(offset), math.log(offset + max_sweep_rate // 2)
return torch.exp(torch.linspace(start, stop, sample_rate, dtype=torch.double)) - offset
def _get_inverse_log_freq(freq, sample_rate, offset):
"""Find the time where the given frequency is given by _get_log_freq"""
half = sample_rate // 2
return sample_rate * (math.log(1 + freq / offset) / math.log(1 + half / offset))
def _get_freq_ticks(sample_rate, offset, f_max):
# Given the original sample rate used for generating the sweep,
# find the x-axis value where the log-scale major frequency values fall in
times, freq = [], []
for exp in range(2, 5):
for v in range(1, 10):
f = v * 10**exp
if f < sample_rate // 2:
t = _get_inverse_log_freq(f, sample_rate, offset) / sample_rate
times.append(t)
freq.append(f)
t_max = _get_inverse_log_freq(f_max, sample_rate, offset) / sample_rate
times.append(t_max)
freq.append(f_max)
return times, freq
def get_sine_sweep(sample_rate, offset=DEFAULT_OFFSET):
max_sweep_rate = sample_rate
freq = _get_log_freq(sample_rate, max_sweep_rate, offset)
delta = 2 * math.pi * freq / sample_rate
cummulative = torch.cumsum(delta, dim=0)
signal = torch.sin(cummulative).unsqueeze(dim=0)
return signal
def plot_sweep(
waveform,
sample_rate,
title,
max_sweep_rate=48000,
offset=DEFAULT_OFFSET,
):
x_ticks = [100, 500, 1000, 5000, 10000, 20000, max_sweep_rate // 2]
y_ticks = [1000, 5000, 10000, 20000, sample_rate // 2]
time, freq = _get_freq_ticks(max_sweep_rate, offset, sample_rate // 2)
freq_x = [f if f in x_ticks and f <= max_sweep_rate // 2 else None for f in freq]
freq_y = [f for f in freq if f in y_ticks and 1000 <= f <= sample_rate // 2]
figure, axis = plt.subplots(1, 1)
_, _, _, cax = axis.specgram(waveform[0].numpy(), Fs=sample_rate)
plt.xticks(time, freq_x)
plt.yticks(freq_y, freq_y)
axis.set_xlabel("Original Signal Frequency (Hz, log scale)")
axis.set_ylabel("Waveform Frequency (Hz)")
axis.xaxis.grid(True, alpha=0.67)
axis.yaxis.grid(True, alpha=0.67)
figure.suptitle(f"{title} (sample rate: {sample_rate} Hz)")
plt.colorbar(cax)
重采样概述¶
要将音频波形从一个频率重采样到另一个频率,您可以使用 torchaudio.transforms.Resample 或 torchaudio.functional.resample()。 transforms.Resample 会预先计算并缓存用于重采样的内核,而 functional.resample 则会即时计算它,因此当使用相同的参数重采样多个波形时,使用 torchaudio.transforms.Resample 会加快速度(参见基准测试部分)。
这两种重采样方法都使用 带限 sinc 插值 来在任意时间点计算信号值。该实现涉及卷积,因此我们可以利用 GPU / 多线程来提高性能。
注意
当在多个子进程中使用重采样时(例如,使用多个工作进程进行数据加载),您的应用程序可能会创建比系统能有效处理的更多的线程。在这种情况下,设置 torch.set_num_threads(1) 可能会有所帮助。
由于有限数量的样本只能表示有限数量的频率,因此重采样不会产生完美的结果,并且可以使用各种参数来控制其质量和计算速度。我们将通过重采样对数正弦扫描(一种频率随时间指数增长的正弦波)来演示这些特性。
下面的频谱图显示了信号的频率表示,其中 x 轴对应原始波形的频率(对数刻度),y 轴对应绘制波形的频率,颜色强度表示振幅。
sample_rate = 48000
waveform = get_sine_sweep(sample_rate)
plot_sweep(waveform, sample_rate, title="Original Waveform")
Audio(waveform.numpy()[0], rate=sample_rate)
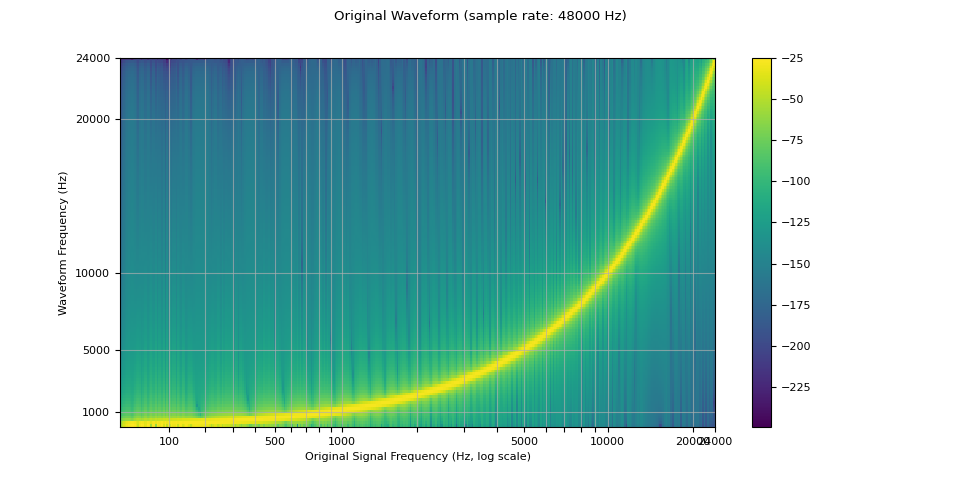
现在我们对其进行重采样(降采样)。
我们看到,在重采样波形的频谱图中,存在一个伪影,而原始波形中没有这个伪影。这种效应称为混叠。 此页面 解释了它是如何发生的,以及为什么它看起来像反射。
resample_rate = 32000
resampler = T.Resample(sample_rate, resample_rate, dtype=waveform.dtype)
resampled_waveform = resampler(waveform)
plot_sweep(resampled_waveform, resample_rate, title="Resampled Waveform")
Audio(resampled_waveform.numpy()[0], rate=resample_rate)
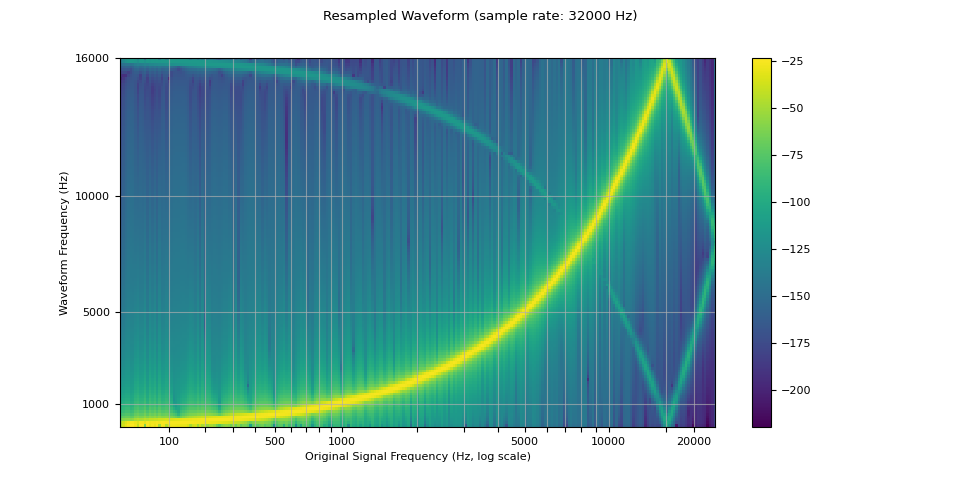
使用参数控制重采样质量¶
低通滤波器宽度¶
由于用于插值的滤波器是无限延伸的,因此 lowpass_filter_width 参数用于控制用于窗口化插值的滤波器的宽度。它也称为零交叉数,因为插值在每个时间单位处通过零。使用较大的 lowpass_filter_width 可提供更清晰、更精确的滤波器,但计算成本更高。
sample_rate = 48000
resample_rate = 32000
resampled_waveform = F.resample(waveform, sample_rate, resample_rate, lowpass_filter_width=6)
plot_sweep(resampled_waveform, resample_rate, title="lowpass_filter_width=6")
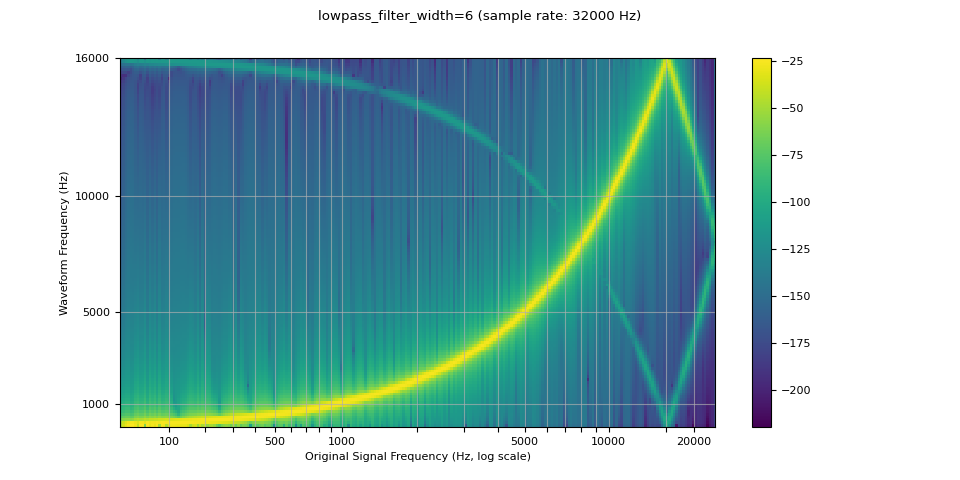
resampled_waveform = F.resample(waveform, sample_rate, resample_rate, lowpass_filter_width=128)
plot_sweep(resampled_waveform, resample_rate, title="lowpass_filter_width=128")
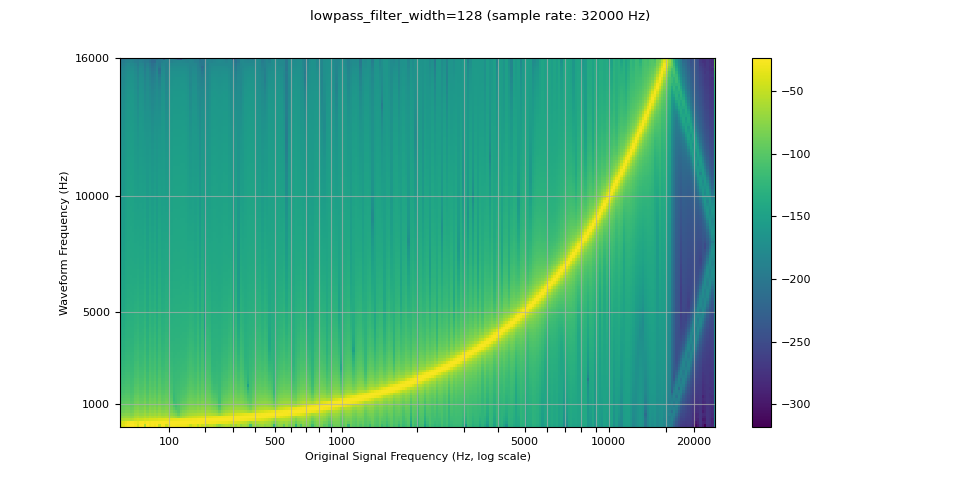
滚降¶
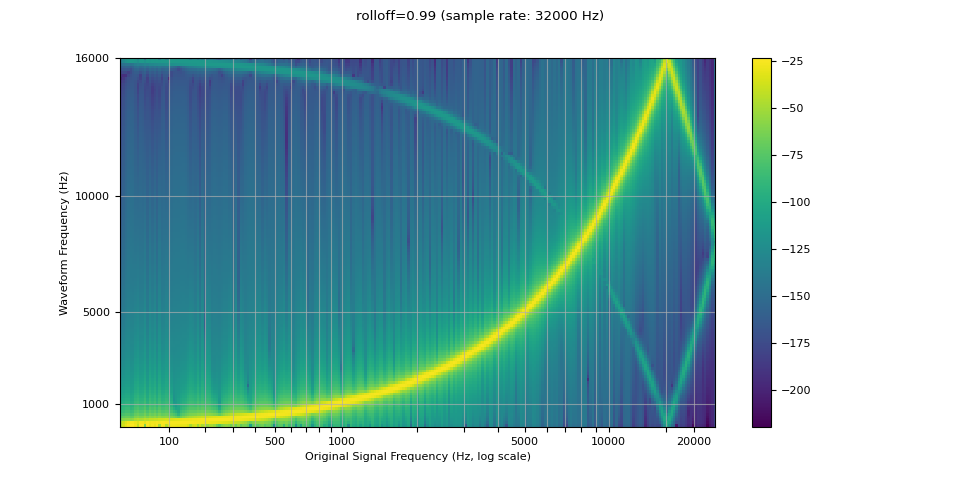
rolloff 参数表示为奈奎斯特频率的分数,奈奎斯特频率是给定有限采样率可表示的最大频率。 rolloff 确定低通滤波器的截止频率,并控制混叠的程度。混叠发生在高于奈奎斯特频率的频率映射到较低频率时。因此,较低的滚降将减少混叠量,但也会减少一些高频分量。
sample_rate = 48000
resample_rate = 32000
resampled_waveform = F.resample(waveform, sample_rate, resample_rate, rolloff=0.99)
plot_sweep(resampled_waveform, resample_rate, title="rolloff=0.99")
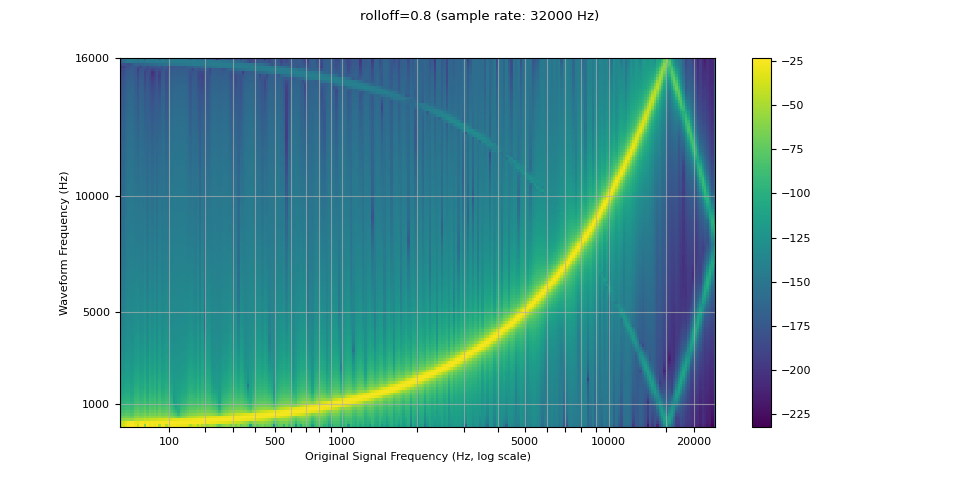
resampled_waveform = F.resample(waveform, sample_rate, resample_rate, rolloff=0.8)
plot_sweep(resampled_waveform, resample_rate, title="rolloff=0.8")
窗函数¶
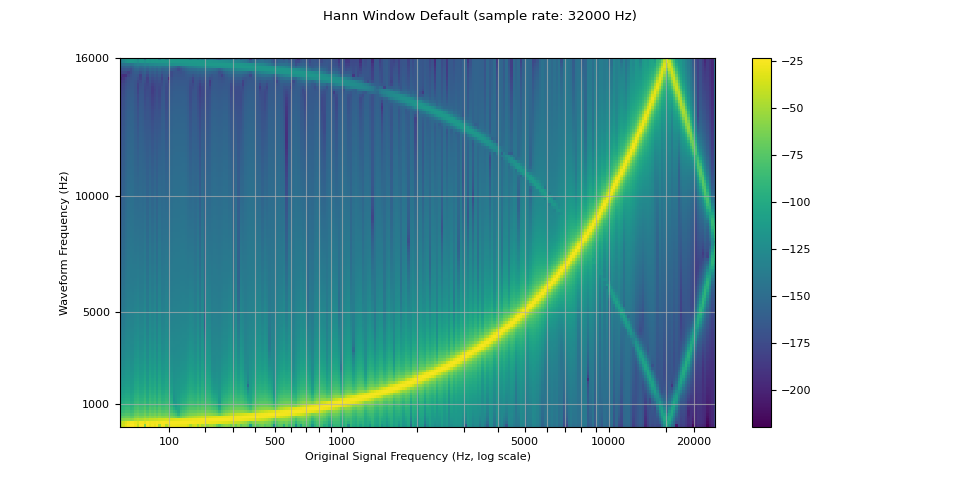
默认情况下,torchaudio 的重采样使用 Hann 窗函数,这是一个加权余弦函数。它还支持 Kaiser 窗,这是一种近乎最优的窗函数,带有一个额外的 beta 参数,允许设计滤波器的平滑度和冲激宽度。这可以通过 resampling_method 参数来控制。
sample_rate = 48000
resample_rate = 32000
resampled_waveform = F.resample(waveform, sample_rate, resample_rate, resampling_method="sinc_interp_hann")
plot_sweep(resampled_waveform, resample_rate, title="Hann Window Default")
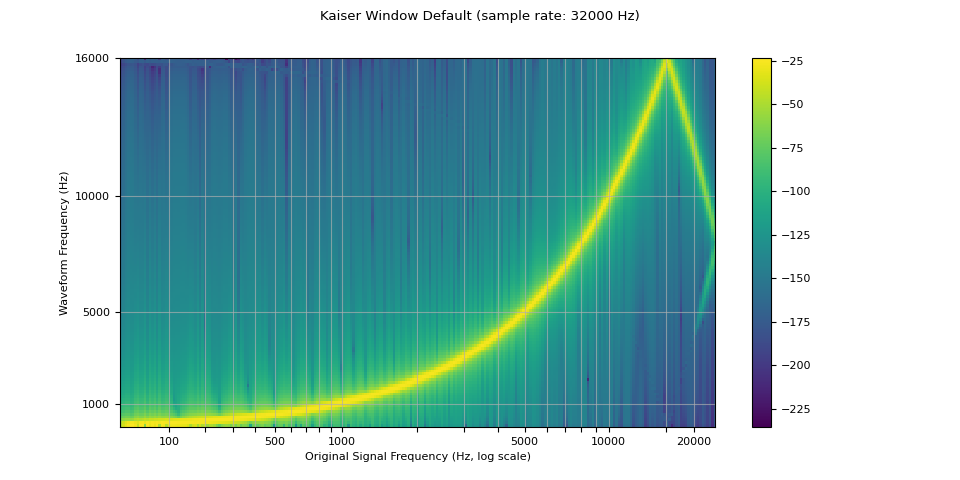
resampled_waveform = F.resample(waveform, sample_rate, resample_rate, resampling_method="sinc_interp_kaiser")
plot_sweep(resampled_waveform, resample_rate, title="Kaiser Window Default")
重采样支持¶
torchaudio 的重采样函数可用于生成与 librosa 的 kaiser 窗重采样类似的结果,但带有一些噪声
sample_rate = 48000
resample_rate = 32000
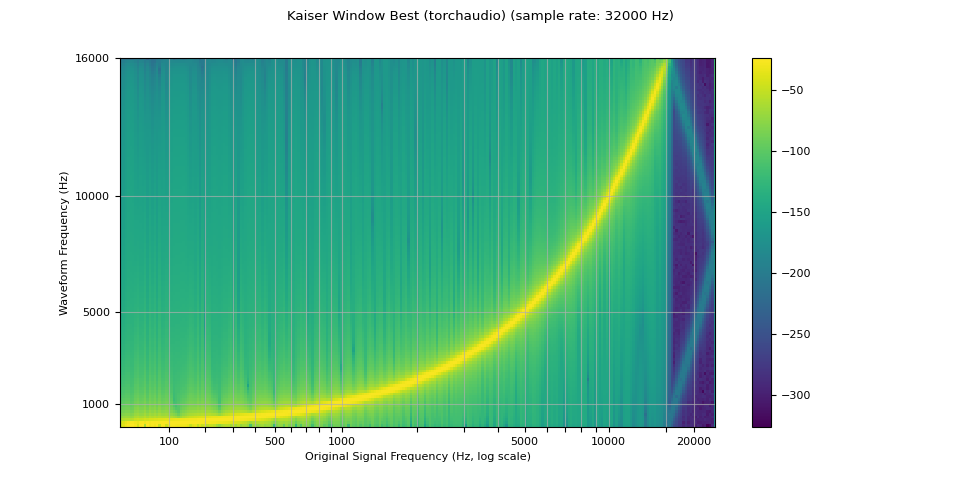
kaiser_best¶
resampled_waveform = F.resample(
waveform,
sample_rate,
resample_rate,
lowpass_filter_width=64,
rolloff=0.9475937167399596,
resampling_method="sinc_interp_kaiser",
beta=14.769656459379492,
)
plot_sweep(resampled_waveform, resample_rate, title="Kaiser Window Best (torchaudio)")
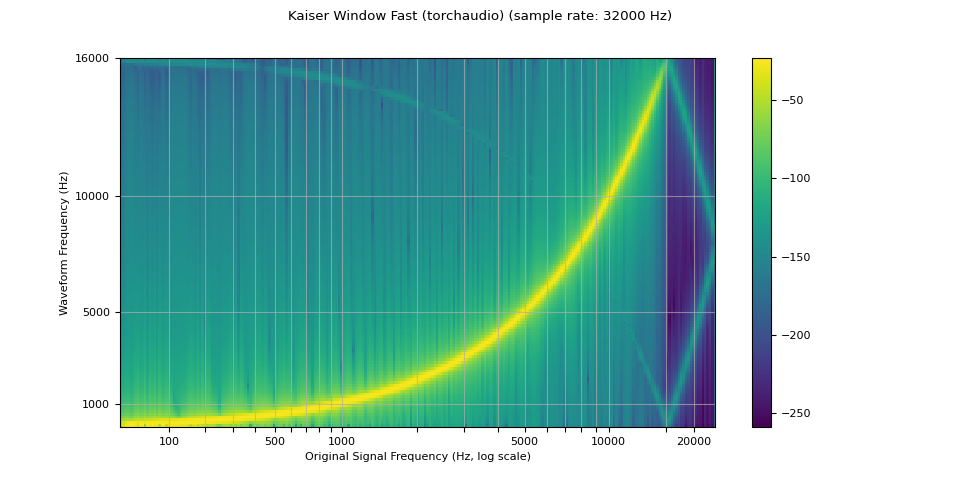
kaiser_fast¶
resampled_waveform = F.resample(
waveform,
sample_rate,
resample_rate,
lowpass_filter_width=16,
rolloff=0.85,
resampling_method="sinc_interp_kaiser",
beta=8.555504641634386,
)
plot_sweep(resampled_waveform, resample_rate, title="Kaiser Window Fast (torchaudio)")
性能基准测试¶
以下是两个采样率对之间的波形降采样和升采样的基准测试。我们展示了 lowpass_filter_width、窗口类型和采样率可能产生的性能影响。
print(f"torchaudio: {torchaudio.__version__}")
torchaudio: 2.8.0a0+1d65bbe
def benchmark_resample_functional(
waveform,
sample_rate,
resample_rate,
lowpass_filter_width=6,
rolloff=0.99,
resampling_method="sinc_interp_hann",
beta=None,
iters=5,
):
return (
timeit.timeit(
stmt="""
torchaudio.functional.resample(
waveform,
sample_rate,
resample_rate,
lowpass_filter_width=lowpass_filter_width,
rolloff=rolloff,
resampling_method=resampling_method,
beta=beta,
)
""",
setup="import torchaudio",
number=iters,
globals=locals(),
)
* 1000
/ iters
)
def benchmark_resample_transforms(
waveform,
sample_rate,
resample_rate,
lowpass_filter_width=6,
rolloff=0.99,
resampling_method="sinc_interp_hann",
beta=None,
iters=5,
):
return (
timeit.timeit(
stmt="resampler(waveform)",
setup="""
import torchaudio
resampler = torchaudio.transforms.Resample(
sample_rate,
resample_rate,
lowpass_filter_width=lowpass_filter_width,
rolloff=rolloff,
resampling_method=resampling_method,
dtype=waveform.dtype,
beta=beta,
)
resampler.to(waveform.device)
""",
number=iters,
globals=locals(),
)
* 1000
/ iters
)
def benchmark(sample_rate, resample_rate):
times, rows = [], []
waveform = get_sine_sweep(sample_rate).to(torch.float32)
args = (waveform, sample_rate, resample_rate)
# sinc 64 zero-crossings
f_time = benchmark_resample_functional(*args, lowpass_filter_width=64)
t_time = benchmark_resample_transforms(*args, lowpass_filter_width=64)
times.append([f_time, t_time])
rows.append("sinc (width 64)")
# sinc 6 zero-crossings
f_time = benchmark_resample_functional(*args, lowpass_filter_width=16)
t_time = benchmark_resample_transforms(*args, lowpass_filter_width=16)
times.append([f_time, t_time])
rows.append("sinc (width 16)")
# kaiser best
kwargs = {
"lowpass_filter_width": 64,
"rolloff": 0.9475937167399596,
"resampling_method": "sinc_interp_kaiser",
"beta": 14.769656459379492,
}
f_time = benchmark_resample_functional(*args, **kwargs)
t_time = benchmark_resample_transforms(*args, **kwargs)
times.append([f_time, t_time])
rows.append("kaiser_best")
# kaiser fast
kwargs = {
"lowpass_filter_width": 16,
"rolloff": 0.85,
"resampling_method": "sinc_interp_kaiser",
"beta": 8.555504641634386,
}
f_time = benchmark_resample_functional(*args, **kwargs)
t_time = benchmark_resample_transforms(*args, **kwargs)
times.append([f_time, t_time])
rows.append("kaiser_fast")
return (np.array(times), ["functional", "transforms"], rows)
def plot(data, cols, rows):
fig, ax = plt.subplots()
x_data = np.arange(len(rows))
bar_width = 0.8 / len(cols)
for (i, (c, d)) in enumerate(zip(cols, data.T)):
x_pos = x_data + (i - len(cols) / 2 + 0.5) * bar_width
ax.bar(x_pos, d, bar_width, label=c)
ax.legend()
ax.set_xticks(x_data)
ax.set_xticklabels(rows)
plt.ylabel("Time Elapsed [ms]")
return ax
降采样(48 -> 44.1 kHz)¶
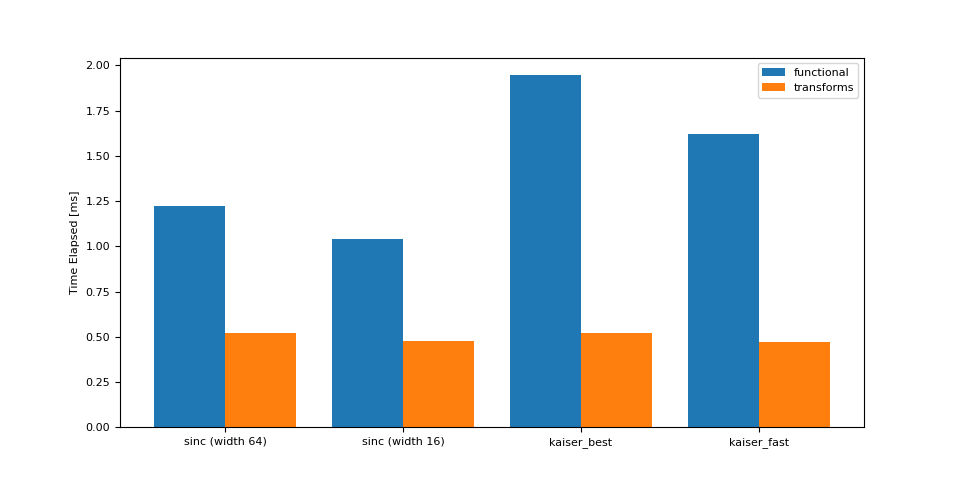
<Axes: ylabel='Time Elapsed [ms]'>
降采样(16 -> 8 kHz)¶
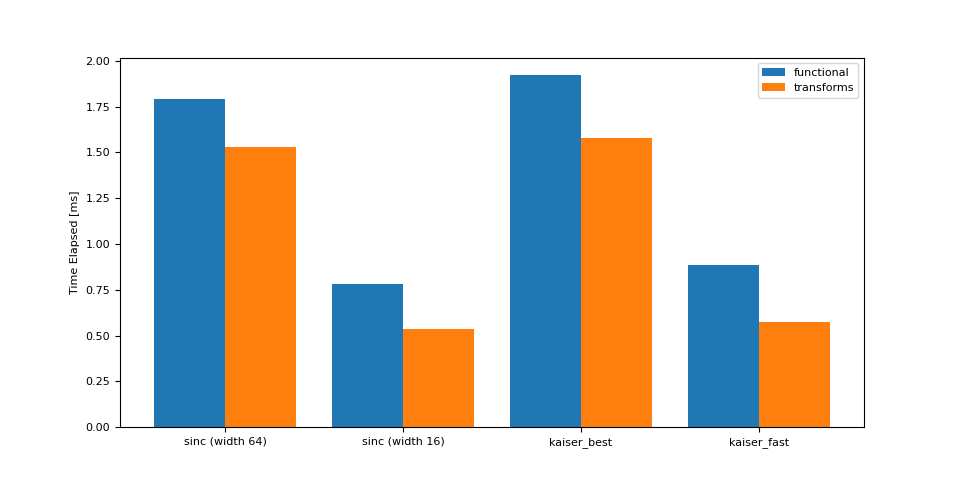
<Axes: ylabel='Time Elapsed [ms]'>
升采样(44.1 -> 48 kHz)¶
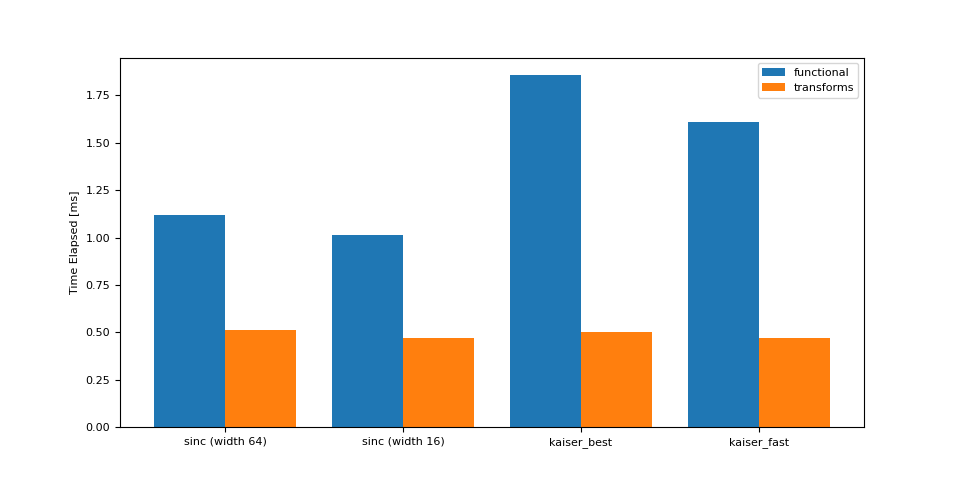
<Axes: ylabel='Time Elapsed [ms]'>
升采样(8 -> 16 kHz)¶
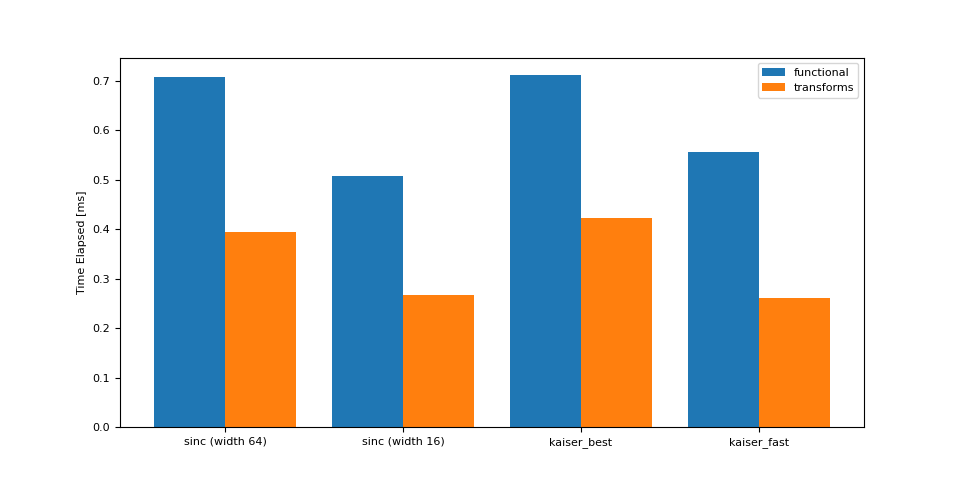
<Axes: ylabel='Time Elapsed [ms]'>
总结¶
进一步阐述结果
较大的
lowpass_filter_width会导致较大的重采样内核,因此会增加内核计算和卷积的计算时间使用
sinc_interp_kaiser的计算时间比默认的sinc_interp_hann长,因为它计算中间窗值更为复杂采样率和重采样率之间较大的 GCD(最大公约数)将导致简化,从而可以使用更小的内核和更快的内核计算。
脚本总运行时间: ( 0 分 2.111 秒)



