beginner/fgsm_tutorial

在 Google Colab 中运行

Colab

下载 Notebook

Notebook

在 GitHub 上查看

GitHub

对抗样本生成

创建时间：2018年8月14日 | 最后更新：2025年1月27日 | 最后验证：未验证

作者： Nathan Inkawhich

如果您正在阅读本文，希望您能认识到一些机器学习模型的有效性。研究不断推动着机器学习模型变得更快、更准确、更高效。然而，在设计和训练模型时，一个常常被忽视的方面是安全性和鲁棒性，尤其是在面对希望愚弄模型的对手时。

本教程将提高您对机器学习模型安全漏洞的认识，并深入探讨对抗性机器学习这一热门话题。您可能会惊讶地发现，向图像添加不易察觉的微小扰动会导致模型性能发生巨大差异。鉴于这是一篇教程，我们将通过一个图像分类器的示例来探讨这个话题。具体来说，我们将使用最早也是最受欢迎的攻击方法之一——快速梯度符号攻击 (FGSM) 来愚弄一个 MNIST 分类器。

威胁模型

为了提供背景信息，存在许多类别的对抗性攻击，每种攻击都有不同的目标和对攻击者知识的假设。然而，总的来说，其总体目标是以最小的扰动修改输入数据以导致期望的错误分类。攻击者的知识存在几种假设，其中两种是：白盒攻击和黑盒攻击。白盒攻击假设攻击者对模型拥有完全的知识和访问权限，包括架构、输入、输出和权重。黑盒攻击假设攻击者只能访问模型的输入和输出，而对底层架构或权重一无所知。目标也有几种类型，包括误分类和源/目标误分类。误分类的目标意味着攻击者只希望输出分类错误，而不关心新的分类是什么。源/目标误分类意味着攻击者希望修改一个最初属于特定源类别的图像，使其被分类为特定的目标类别。

在这种情况下，FGSM 攻击是一种以误分类为目标的白盒攻击。有了这些背景信息，我们现在可以详细讨论该攻击。

快速梯度符号攻击

目前最早也是最受欢迎的对抗性攻击之一被称为快速梯度符号攻击 (FGSM)，由 Goodfellow 等人在 《解释和利用对抗样本》 中进行了描述。这种攻击异常强大，却又直观。它利用神经网络的学习方式——梯度——来攻击它们。思路很简单，攻击不是通过基于反向传播的梯度调整权重来最小化损失，而是基于相同的反向传播梯度，调整输入数据以最大化损失。换句话说，攻击使用损失关于输入数据的梯度，然后调整输入数据以最大化损失。

在开始编写代码之前，让我们看一下著名的 FGSM 熊猫示例，并提取一些符号。

从图中可以看出，\(\mathbf{x}\) 是被正确分类为“熊猫”的原始输入图像，\(y\) 是 \(\mathbf{x}\) 的真实标签，\(\mathbf{\theta}\) 表示模型参数，而 \(\mathbf{J}(\mathbf{\theta}, \mathbf{x}, y)\) 是用于训练网络的损失。攻击将梯度反向传播到输入数据以计算 \(\nabla_{x} J(\mathbf{\theta}, \mathbf{x}, y)\)。然后，它沿最大化损失的方向（即 \(sign(\nabla_{x} J(\mathbf{\theta}, \mathbf{x}, y))\)）以一个小的步长（图片中为 \(\epsilon\) 或 \(0.007\)）调整输入数据。得到的扰动图像 \(x'\)，然后被目标网络误分类为“长臂猿”，尽管它仍然明显是“熊猫”。

希望现在本教程的动机已经很清楚了，那么让我们开始实现。

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
import numpy as np
import matplotlib.pyplot as plt

实现

在本节中，我们将讨论本教程的输入参数，定义被攻击的模型，然后编写攻击代码并运行一些测试。

输入

本教程只有三个输入，定义如下：

• epsilons - 用于运行的 epsilon 值列表。在列表中包含 0 很重要，因为它代表模型在原始测试集上的性能。此外，直观上我们期望 epsilon 值越大，扰动越明显，但攻击在降低模型准确性方面越有效。由于这里的数据范围是 \([0,1]\)，任何 epsilon 值都不应超过 1。

• pretrained_model - 预训练的 MNIST 模型路径，该模型使用 pytorch/examples/mnist 进行训练。为简单起见，请在此处 下载 预训练模型。

epsilons = [0, .05, .1, .15, .2, .25, .3]
pretrained_model = "data/lenet_mnist_model.pth"
# Set random seed for reproducibility
torch.manual_seed(42)

<torch._C.Generator object at 0x7fe4953749b0>

被攻击的模型

如前所述，被攻击的模型与 pytorch/examples/mnist 中的 MNIST 模型相同。您可以训练并保存自己的 MNIST 模型，也可以下载并使用提供的模型。这里的Net定义和测试数据加载器是从 MNIST 示例中复制的。本节的目的是定义模型和数据加载器，然后初始化模型并加载预训练权重。

# LeNet Model definition
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(1, 32, 3, 1)
        self.conv2 = nn.Conv2d(32, 64, 3, 1)
        self.dropout1 = nn.Dropout(0.25)
        self.dropout2 = nn.Dropout(0.5)
        self.fc1 = nn.Linear(9216, 128)
        self.fc2 = nn.Linear(128, 10)

    def forward(self, x):
        x = self.conv1(x)
        x = F.relu(x)
        x = self.conv2(x)
        x = F.relu(x)
        x = F.max_pool2d(x, 2)
        x = self.dropout1(x)
        x = torch.flatten(x, 1)
        x = self.fc1(x)
        x = F.relu(x)
        x = self.dropout2(x)
        x = self.fc2(x)
        output = F.log_softmax(x, dim=1)
        return output

# MNIST Test dataset and dataloader declaration
test_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=False, download=True, transform=transforms.Compose([
            transforms.ToTensor(),
            transforms.Normalize((0.1307,), (0.3081,)),
            ])),
        batch_size=1, shuffle=True)

# We want to be able to train our model on an `accelerator <https://pytorch.ac.cn/docs/stable/torch.html#accelerators>`__
# such as CUDA, MPS, MTIA, or XPU. If the current accelerator is available, we will use it. Otherwise, we use the CPU.
device = torch.accelerator.current_accelerator().type if torch.accelerator.is_available() else "cpu"
print(f"Using {device} device")

# Initialize the network
model = Net().to(device)

# Load the pretrained model
model.load_state_dict(torch.load(pretrained_model, map_location=device, weights_only=True))

# Set the model in evaluation mode. In this case this is for the Dropout layers
model.eval()

  0%|          | 0.00/9.91M [00:00<?, ?B/s]
100%|██████████| 9.91M/9.91M [00:00<00:00, 128MB/s]

  0%|          | 0.00/28.9k [00:00<?, ?B/s]
100%|██████████| 28.9k/28.9k [00:00<00:00, 31.9MB/s]

  0%|          | 0.00/1.65M [00:00<?, ?B/s]
100%|██████████| 1.65M/1.65M [00:00<00:00, 164MB/s]

  0%|          | 0.00/4.54k [00:00<?, ?B/s]
100%|██████████| 4.54k/4.54k [00:00<00:00, 27.4MB/s]
Using cuda device

Net(
  (conv1): Conv2d(1, 32, kernel_size=(3, 3), stride=(1, 1))
  (conv2): Conv2d(32, 64, kernel_size=(3, 3), stride=(1, 1))
  (dropout1): Dropout(p=0.25, inplace=False)
  (dropout2): Dropout(p=0.5, inplace=False)
  (fc1): Linear(in_features=9216, out_features=128, bias=True)
  (fc2): Linear(in_features=128, out_features=10, bias=True)
)

FGSM 攻击

现在，我们可以定义通过扰动原始输入来创建对抗样本的函数。 fgsm_attack 函数接受三个输入：image 是原始的干净图像 (\(x\))，epsilon 是像素扰动量 (\(\epsilon\))，data_grad 是损失关于输入图像的梯度 (\(\nabla_{x} J(\mathbf{\theta}, \mathbf{x}, y)\))。然后，该函数创建扰动图像，如下所示：

\[perturbed\_image = image + epsilon*sign(data\_grad) = x + \epsilon * sign(\nabla_{x} J(\mathbf{\theta}, \mathbf{x}, y)) \]

最后，为了保持数据的原始范围，将扰动后的图像裁剪到 \([0,1]\) 范围内。

# FGSM attack code
def fgsm_attack(image, epsilon, data_grad):
    # Collect the element-wise sign of the data gradient
    sign_data_grad = data_grad.sign()
    # Create the perturbed image by adjusting each pixel of the input image
    perturbed_image = image + epsilon*sign_data_grad
    # Adding clipping to maintain [0,1] range
    perturbed_image = torch.clamp(perturbed_image, 0, 1)
    # Return the perturbed image
    return perturbed_image

# restores the tensors to their original scale
def denorm(batch, mean=[0.1307], std=[0.3081]):
    """
    Convert a batch of tensors to their original scale.

    Args:
        batch (torch.Tensor): Batch of normalized tensors.
        mean (torch.Tensor or list): Mean used for normalization.
        std (torch.Tensor or list): Standard deviation used for normalization.

    Returns:
        torch.Tensor: batch of tensors without normalization applied to them.
    """
    if isinstance(mean, list):
        mean = torch.tensor(mean).to(device)
    if isinstance(std, list):
        std = torch.tensor(std).to(device)

    return batch * std.view(1, -1, 1, 1) + mean.view(1, -1, 1, 1)

测试函数

最后，本教程的核心结果来自 test 函数。每次调用此测试函数都会在 MNIST 测试集上执行完整的测试步骤并报告最终准确率。但是，请注意，此函数还接受一个epsilon输入。这是因为 test 函数报告了在 \(\epsilon\) 强度下受到攻击的模型的准确率。更具体地说，对于测试集中的每个样本，该函数计算损失关于输入数据的梯度（\(data\_grad\)），使用 fgsm_attack 创建扰动图像（\(perturbed\_data\)），然后检查扰动后的样本是否具有对抗性。除了测试模型的准确率外，该函数还保存并返回一些成功的对抗样本，以便稍后进行可视化。

def test( model, device, test_loader, epsilon ):

    # Accuracy counter
    correct = 0
    adv_examples = []

    # Loop over all examples in test set
    for data, target in test_loader:

        # Send the data and label to the device
        data, target = data.to(device), target.to(device)

        # Set requires_grad attribute of tensor. Important for Attack
        data.requires_grad = True

        # Forward pass the data through the model
        output = model(data)
        init_pred = output.max(1, keepdim=True)[1] # get the index of the max log-probability

        # If the initial prediction is wrong, don't bother attacking, just move on
        if init_pred.item() != target.item():
            continue

        # Calculate the loss
        loss = F.nll_loss(output, target)

        # Zero all existing gradients
        model.zero_grad()

        # Calculate gradients of model in backward pass
        loss.backward()

        # Collect ``datagrad``
        data_grad = data.grad.data

        # Restore the data to its original scale
        data_denorm = denorm(data)

        # Call FGSM Attack
        perturbed_data = fgsm_attack(data_denorm, epsilon, data_grad)

        # Reapply normalization
        perturbed_data_normalized = transforms.Normalize((0.1307,), (0.3081,))(perturbed_data)

        # Re-classify the perturbed image
        output = model(perturbed_data_normalized)

        # Check for success
        final_pred = output.max(1, keepdim=True)[1] # get the index of the max log-probability
        if final_pred.item() == target.item():
            correct += 1
            # Special case for saving 0 epsilon examples
            if epsilon == 0 and len(adv_examples) < 5:
                adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
                adv_examples.append( (init_pred.item(), final_pred.item(), adv_ex) )
        else:
            # Save some adv examples for visualization later
            if len(adv_examples) < 5:
                adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
                adv_examples.append( (init_pred.item(), final_pred.item(), adv_ex) )

    # Calculate final accuracy for this epsilon
    final_acc = correct/float(len(test_loader))
    print(f"Epsilon: {epsilon}\tTest Accuracy = {correct} / {len(test_loader)} = {final_acc}")

    # Return the accuracy and an adversarial example
    return final_acc, adv_examples

运行攻击

实现部分的最后一步是实际运行攻击。在这里，我们对epsilons输入中的每个 epsilon 值运行一个完整的测试步骤。对于每个 epsilon，我们还保存最终的准确率和一些成功的对抗样本，以便在接下来的部分进行绘制。请注意，随着 epsilon 值的增加，打印出的准确率如何下降。另外，请注意 \(\epsilon=0\) 的情况代表原始测试准确率，没有受到攻击。

accuracies = []
examples = []

# Run test for each epsilon
for eps in epsilons:
    acc, ex = test(model, device, test_loader, eps)
    accuracies.append(acc)
    examples.append(ex)

Epsilon: 0      Test Accuracy = 9912 / 10000 = 0.9912
Epsilon: 0.05   Test Accuracy = 9605 / 10000 = 0.9605
Epsilon: 0.1    Test Accuracy = 8743 / 10000 = 0.8743
Epsilon: 0.15   Test Accuracy = 7108 / 10000 = 0.7108
Epsilon: 0.2    Test Accuracy = 4859 / 10000 = 0.4859
Epsilon: 0.25   Test Accuracy = 2718 / 10000 = 0.2718
Epsilon: 0.3    Test Accuracy = 1411 / 10000 = 0.1411

结果

准确率与 Epsilon 的关系

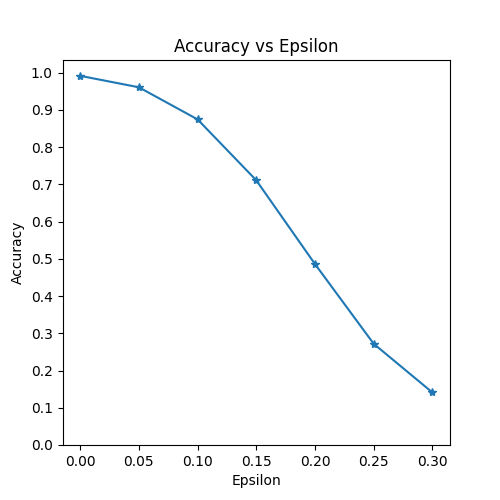
第一个结果是准确率与 epsilon 的关系图。如前所述，随着 epsilon 的增加，我们期望测试准确率下降。这是因为更大的 epsilon 意味着我们在最大化损失的方向上迈出更大的步子。请注意，尽管 epsilon 值是线性间隔的，但曲线的趋势并非线性。例如，\(\epsilon=0.05\) 时的准确率仅比 \(\epsilon=0\) 时低约 4%，而 \(\epsilon=0.2\) 时的准确率比 \(\epsilon=0.15\) 时低 25%。另外，请注意，模型在 \(\epsilon=0.25\) 和 \(\epsilon=0.3\) 之间的准确率达到了 10 类分类器的随机准确率。

plt.figure(figsize=(5,5))
plt.plot(epsilons, accuracies, "*-")
plt.yticks(np.arange(0, 1.1, step=0.1))
plt.xticks(np.arange(0, .35, step=0.05))
plt.title("Accuracy vs Epsilon")
plt.xlabel("Epsilon")
plt.ylabel("Accuracy")
plt.show()

示例对抗样本

还记得“天下没有免费的午餐”吗？在这种情况下，随着 epsilon 的增加，测试准确率下降，但是扰动也更容易被察觉。实际上，在准确率下降和可感知性之间存在一个权衡，攻击者必须考虑这一点。在这里，我们展示了一些在每个 epsilon 值下的成功对抗样本的例子。绘图的每一行都显示了一个不同的 epsilon 值。第一行是 \(\epsilon=0\) 的示例，代表没有扰动的原始“干净”图像。每张图像的标题显示“原始分类 -> 对抗性分类”。请注意，在 \(\epsilon=0.15\) 时，扰动开始变得明显，而在 \(\epsilon=0.3\) 时则非常明显。然而，在所有情况下，人类仍然能够识别正确的类别，尽管添加了噪声。

# Plot several examples of adversarial samples at each epsilon
cnt = 0
plt.figure(figsize=(8,10))
for i in range(len(epsilons)):
    for j in range(len(examples[i])):
        cnt += 1
        plt.subplot(len(epsilons),len(examples[0]),cnt)
        plt.xticks([], [])
        plt.yticks([], [])
        if j == 0:
            plt.ylabel(f"Eps: {epsilons[i]}", fontsize=14)
        orig,adv,ex = examples[i][j]
        plt.title(f"{orig} -> {adv}")
        plt.imshow(ex, cmap="gray")
plt.tight_layout()
plt.show()

下一步去哪儿？

希望本教程能让您对对抗性机器学习这一主题有所了解。从这里可以有很多潜在的方向。这种攻击代表了对抗性攻击研究的开端，此后出现了许多关于如何从攻击者那里攻击和防御机器学习模型的后续想法。事实上，在 NIPS 2017 上曾举办过一次对抗性攻击和防御竞赛，竞赛中使用的许多方法都在这篇论文中进行了描述：对抗性攻击和防御竞赛。防御工作也引出了使机器学习模型整体上更加鲁棒的想法，无论是对自然扰动输入还是对抗性精心设计的输入。

另一个方向是不同领域的对抗性攻击和防御。对抗性研究不仅限于图像领域，请查看 这项 对语音转文本模型的攻击。但或许了解对抗性机器学习的最好方法是亲自动手实践。尝试实现 NIPS 2017 竞赛中的另一种攻击，看看它与 FGSM 有何不同。然后，尝试从您自己的攻击中防御模型。

另一个方向，取决于可用资源，是修改代码以支持批处理、并行和/或分布式处理工作，而不是在上面的每个 epsilon test() 循环中一次处理一个攻击。