


注意
跳转至结尾 下载完整的示例代码。
简介 || 张量 || Autograd || 构建模型 || TensorBoard 支持 || 训练模型 || 模型理解
Autograd 的基础#
创建于:2021 年 11 月 30 日 | 最后更新:2024 年 2 月 26 日 | 最后验证:2024 年 11 月 05 日
请跟随下面的视频或在 youtube 上观看。
PyTorch 的 *Autograd* 功能是 PyTorch 在构建机器学习项目时之所以灵活且快速的原因之一。它能够快速轻松地对复杂计算进行多次偏导数(也称为 *梯度*)的计算。此操作是基于反向传播的神经网络学习的核心。
Autograd 的强大之处在于它能在 *运行时* 动态追踪你的计算,这意味着如果你的模型有决策分支,或者循环的长度直到运行时才能确定,计算仍然会被正确追踪,并且你将获得正确的梯度来驱动学习。这一点,再加上你的模型是用 Python 构建的事实,提供了比依赖于对更刚性结构的模型的静态分析来计算梯度的框架更大的灵活性。
我们需要 Autograd 来做什么?#
机器学习模型是一个*函数*,具有输入和输出。在本讨论中,我们将输入视为一个*i*维向量 \(\vec{x}\),其元素为 \(x_{i}\)。然后,我们可以将模型 *M* 表示为输入的向量值函数:\(\vec{y} = \vec{M}(\vec{x})\)。 (我们将 M 的输出值视为向量,因为 M 通常可能具有任意数量的输出。)
由于我们主要将在训练的上下文中讨论 autograd,因此我们关心的输出将是模型的损失。*损失函数* L(\(\vec{y}\)) = L(\(\vec{M}\)(\(\vec{x}\))) 是模型输出的单个标量函数。此函数表达了模型的预测与特定输入的*理想*输出之间的差距。*注意:在此之后,我们将经常省略向量符号,只要上下文清晰即可 - 例如,* \(y\) 而不是 \(\vec y\)。
在训练模型时,我们希望最小化损失。在理想的完美模型情况下,这意味着调整其学习权重 - 即函数的可调参数 - 以使所有输入的损失为零。在实际世界中,这意味着一个迭代过程,即不断调整学习权重,直到我们看到对于各种输入都能获得可接受的损失。
我们如何决定如何调整权重以及调整哪个方向?我们想*最小化*损失,这意味着使其关于输入的第一个导数等于 0:\(\frac{\partial L}{\partial x} = 0\)。
但是,请记住,损失不是*直接*从输入派生的,而是模型输出(它是输入的函数)的函数,\(\frac{\partial L}{\partial x}\) = \(\frac{\partial {L({\vec y})}}{\partial x}\)。根据微分学的链式法则,我们有 \(\frac{\partial {L({\vec y})}}{\partial x}\) = \(\frac{\partial L}{\partial y}\frac{\partial y}{\partial x}\) = \(\frac{\partial L}{\partial y}\frac{\partial M(x)}{\partial x}\)。
\(\frac{\partial M(x)}{\partial x}\) 是事情变得复杂的地方。模型输出关于其输入的偏导数,如果我们再次使用链式法则展开表达式,将涉及关于每个乘法的学习权重、每个激活函数以及模型中的每个其他数学变换的许多局部偏导数。每个此类偏导数的完整表达式是*每条可能路径*通过计算图的局部梯度的乘积之和,该路径以我们正在尝试度量的变量的梯度为终点。
特别重要的是,关于学习权重的梯度对我们很重要 - 它们告诉我们*改变每个权重的方向*以使损失函数更接近零。
由于这些局部导数的数量(每个导数对应于模型计算图中的一条独立路径)往往随着神经网络的深度呈指数级增长,因此计算它们的复杂性也随之增加。这就是 autograd 发挥作用的地方:它会追踪每个计算的历史。你 PyTorch 模型中的每个计算出的张量都带有其输入张量和创建它的函数的历史记录。结合 PyTorch 中用于对张量进行操作的函数都具有计算自身导数的内置实现这一事实,这大大加快了计算学习所需的局部导数的速度。
一个简单的例子#
理论讲了很多 - 但在实践中使用 autograd 是什么样的?
让我们从一个简单的例子开始。首先,我们将进行一些导入,以便我们可以绘制我们的结果
# %matplotlib inline
import torch
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
import math
接下来,我们将创建一个包含 \([0, 2\pi]\) 区间内等距值的输入张量,并指定 `requires_grad=True`。(与大多数创建张量的函数一样,`torch.linspace()` 接受可选的 `requires_grad` 选项。)设置此标志意味着在之后的每次计算中,autograd 都将累积该计算的输出张量中的计算历史。
a = torch.linspace(0., 2. * math.pi, steps=25, requires_grad=True)
print(a)
tensor([0.0000, 0.2618, 0.5236, 0.7854, 1.0472, 1.3090, 1.5708, 1.8326, 2.0944,
2.3562, 2.6180, 2.8798, 3.1416, 3.4034, 3.6652, 3.9270, 4.1888, 4.4506,
4.7124, 4.9742, 5.2360, 5.4978, 5.7596, 6.0214, 6.2832],
requires_grad=True)
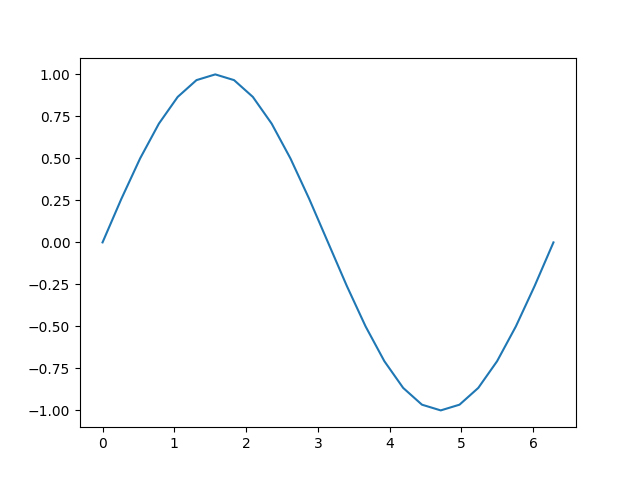
接下来,我们将执行一个计算,并绘制其输出相对于其输入的图
[<matplotlib.lines.Line2D object at 0x7f49b5981750>]
让我们仔细看看张量 `b`。当我们打印它时,我们会看到一个指示器,表明它正在追踪计算历史
print(b)
tensor([ 0.0000e+00, 2.5882e-01, 5.0000e-01, 7.0711e-01, 8.6603e-01,
9.6593e-01, 1.0000e+00, 9.6593e-01, 8.6603e-01, 7.0711e-01,
5.0000e-01, 2.5882e-01, -8.7423e-08, -2.5882e-01, -5.0000e-01,
-7.0711e-01, -8.6603e-01, -9.6593e-01, -1.0000e+00, -9.6593e-01,
-8.6603e-01, -7.0711e-01, -5.0000e-01, -2.5882e-01, 1.7485e-07],
grad_fn=<SinBackward0>)
这个 `grad_fn` 给了我们一个提示,当我们执行反向传播步骤并计算梯度时,我们需要计算此张量所有输入的 \(\sin(x)\) 的导数。
让我们进行更多计算
tensor([ 0.0000e+00, 5.1764e-01, 1.0000e+00, 1.4142e+00, 1.7321e+00,
1.9319e+00, 2.0000e+00, 1.9319e+00, 1.7321e+00, 1.4142e+00,
1.0000e+00, 5.1764e-01, -1.7485e-07, -5.1764e-01, -1.0000e+00,
-1.4142e+00, -1.7321e+00, -1.9319e+00, -2.0000e+00, -1.9319e+00,
-1.7321e+00, -1.4142e+00, -1.0000e+00, -5.1764e-01, 3.4969e-07],
grad_fn=<MulBackward0>)
tensor([ 1.0000e+00, 1.5176e+00, 2.0000e+00, 2.4142e+00, 2.7321e+00,
2.9319e+00, 3.0000e+00, 2.9319e+00, 2.7321e+00, 2.4142e+00,
2.0000e+00, 1.5176e+00, 1.0000e+00, 4.8236e-01, -3.5763e-07,
-4.1421e-01, -7.3205e-01, -9.3185e-01, -1.0000e+00, -9.3185e-01,
-7.3205e-01, -4.1421e-01, 4.7684e-07, 4.8236e-01, 1.0000e+00],
grad_fn=<AddBackward0>)
最后,让我们计算一个单元素输出。当你对没有参数的张量调用 `.backward()` 时,它期望调用张量只包含一个元素,就像计算损失函数时一样。
tensor(25., grad_fn=<SumBackward0>)
我们张量中存储的每个 `grad_fn` 都允许你通过其 `next_functions` 属性将计算完全回溯到其输入。我们可以在下面看到,通过此属性深入 `d` 可以显示所有先前张量的梯度函数。请注意,`a.grad_fn` 被报告为 `None`,这表明它是函数的输入,没有自己的历史记录。
print('d:')
print(d.grad_fn)
print(d.grad_fn.next_functions)
print(d.grad_fn.next_functions[0][0].next_functions)
print(d.grad_fn.next_functions[0][0].next_functions[0][0].next_functions)
print(d.grad_fn.next_functions[0][0].next_functions[0][0].next_functions[0][0].next_functions)
print('\nc:')
print(c.grad_fn)
print('\nb:')
print(b.grad_fn)
print('\na:')
print(a.grad_fn)
d:
<AddBackward0 object at 0x7f497c1b9ae0>
((<MulBackward0 object at 0x7f49741dc610>, 0), (None, 0))
((<SinBackward0 object at 0x7f49741dc610>, 0), (None, 0))
((<AccumulateGrad object at 0x7f497c1b9ae0>, 0),)
()
c:
<MulBackward0 object at 0x7f49741dc610>
b:
<SinBackward0 object at 0x7f49741dc610>
a:
None
有了所有这些机制,我们如何获得导数?你调用输出上的 `backward()` 方法,并检查输入的 `grad` 属性来检查梯度
out.backward()
print(a.grad)
plt.plot(a.detach(), a.grad.detach())
tensor([ 2.0000e+00, 1.9319e+00, 1.7321e+00, 1.4142e+00, 1.0000e+00,
5.1764e-01, -8.7423e-08, -5.1764e-01, -1.0000e+00, -1.4142e+00,
-1.7321e+00, -1.9319e+00, -2.0000e+00, -1.9319e+00, -1.7321e+00,
-1.4142e+00, -1.0000e+00, -5.1764e-01, 2.3850e-08, 5.1764e-01,
1.0000e+00, 1.4142e+00, 1.7321e+00, 1.9319e+00, 2.0000e+00])
[<matplotlib.lines.Line2D object at 0x7f49b4dec4c0>]
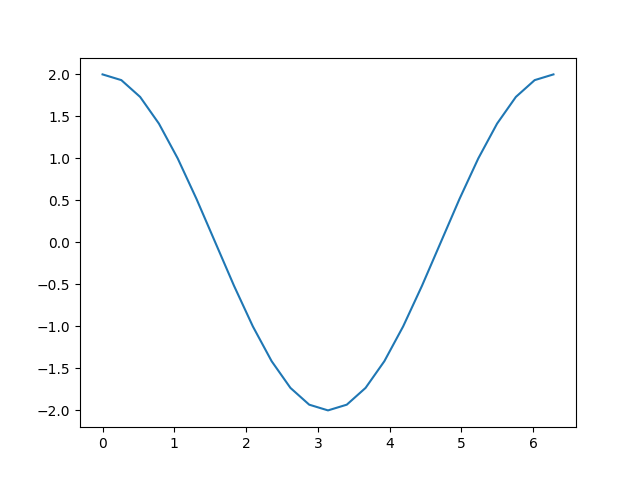
回想一下我们为得到这里所采取的计算步骤
添加一个常量,就像我们计算 `d` 时所做的一样,不会改变导数。这就剩下 \(c = 2 * b = 2 * \sin(a)\),其导数应该是 \(2 * \cos(a)\)。查看上面的图,这正是我们看到的。
请注意,只有计算的*叶子节点*才计算其梯度。例如,如果你尝试 `print(c.grad)`,你将得到 `None`。在这个简单的例子中,只有输入是叶子节点,因此只有它计算了梯度。
训练中的 Autograd#
我们简要了解了 autograd 的工作原理,但它在其预期用途中看起来是什么样的?让我们定义一个小型模型并检查它在单个训练批次后的变化。首先,定义一些常量、我们的模型以及输入和输出的一些占位符
BATCH_SIZE = 16
DIM_IN = 1000
HIDDEN_SIZE = 100
DIM_OUT = 10
class TinyModel(torch.nn.Module):
def __init__(self):
super(TinyModel, self).__init__()
self.layer1 = torch.nn.Linear(DIM_IN, HIDDEN_SIZE)
self.relu = torch.nn.ReLU()
self.layer2 = torch.nn.Linear(HIDDEN_SIZE, DIM_OUT)
def forward(self, x):
x = self.layer1(x)
x = self.relu(x)
x = self.layer2(x)
return x
some_input = torch.randn(BATCH_SIZE, DIM_IN, requires_grad=False)
ideal_output = torch.randn(BATCH_SIZE, DIM_OUT, requires_grad=False)
model = TinyModel()
你可能会注意到的一件事是我们从未为模型的层指定 `requires_grad=True`。在 `torch.nn.Module` 的子类中,我们假设我们想要跟踪层权重的梯度以用于学习。
如果我们查看模型的层,我们可以检查权值的值,并验证尚未计算任何梯度
print(model.layer2.weight[0][0:10]) # just a small slice
print(model.layer2.weight.grad)
tensor([ 0.0328, -0.0364, -0.0408, -0.0376, 0.0818, 0.0147, -0.0665, 0.0056,
-0.0273, -0.0751], grad_fn=<SliceBackward0>)
None
让我们看看当我们在一个训练批次中运行时会发生什么。对于损失函数,我们将使用我们 `prediction` 和 `ideal_output` 之间的欧几里得距离的平方,并且我们将使用一个基本的随机梯度下降优化器。
optimizer = torch.optim.SGD(model.parameters(), lr=0.001)
prediction = model(some_input)
loss = (ideal_output - prediction).pow(2).sum()
print(loss)
tensor(157.6906, grad_fn=<SumBackward0>)
现在,让我们调用 `loss.backward()` 看看会发生什么
loss.backward()
print(model.layer2.weight[0][0:10])
print(model.layer2.weight.grad[0][0:10])
tensor([ 0.0328, -0.0364, -0.0408, -0.0376, 0.0818, 0.0147, -0.0665, 0.0056,
-0.0273, -0.0751], grad_fn=<SliceBackward0>)
tensor([ -3.3823, -5.1896, -10.4124, -6.9933, -4.6069, -2.6109, -0.1184,
-3.4189, -3.9634, -1.2222])
我们可以看到每个学习权重的梯度都被计算出来了,但权重保持不变,因为我们还没有运行优化器。优化器负责根据计算出的梯度更新模型权重。
optimizer.step()
print(model.layer2.weight[0][0:10])
print(model.layer2.weight.grad[0][0:10])
tensor([ 0.0361, -0.0312, -0.0304, -0.0306, 0.0864, 0.0173, -0.0663, 0.0090,
-0.0233, -0.0738], grad_fn=<SliceBackward0>)
tensor([ -3.3823, -5.1896, -10.4124, -6.9933, -4.6069, -2.6109, -0.1184,
-3.4189, -3.9634, -1.2222])
你应该会看到 `layer2` 的权重已更改。
关于这个过程的一个重要事项:调用 `optimizer.step()` 后,你需要调用 `optimizer.zero_grad()`,否则每次运行 `loss.backward()` 时,学习权重的梯度都会累积
print(model.layer2.weight.grad[0][0:10])
for i in range(0, 5):
prediction = model(some_input)
loss = (ideal_output - prediction).pow(2).sum()
loss.backward()
print(model.layer2.weight.grad[0][0:10])
optimizer.zero_grad(set_to_none=False)
print(model.layer2.weight.grad[0][0:10])
tensor([ -3.3823, -5.1896, -10.4124, -6.9933, -4.6069, -2.6109, -0.1184,
-3.4189, -3.9634, -1.2222])
tensor([ -7.5784, -15.7621, -31.9912, -17.6633, -14.4308, -14.5418, 9.5047,
-7.6611, -11.0979, -1.2838])
tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
运行上面的单元格后,你应该会看到,在多次运行 `loss.backward()` 后,大多数梯度的幅度会大得多。在运行下一个训练批次之前未能清零梯度会导致梯度以这种方式爆炸,导致不正确和不可预测的学习结果。
关闭和打开 Autograd#
在某些情况下,你需要精细控制 autograd 是否启用。根据情况,有多种方法可以做到这一点。
最简单的方法是直接更改张量上的 `requires_grad` 标志
tensor([[1., 1., 1.],
[1., 1., 1.]], requires_grad=True)
tensor([[2., 2., 2.],
[2., 2., 2.]], grad_fn=<MulBackward0>)
tensor([[2., 2., 2.],
[2., 2., 2.]])
在上面的单元格中,我们看到 `b1` 有一个 `grad_fn`(即,一个被追踪的计算历史),这符合我们的预期,因为它源自一个具有 autograd 打开的张量 `a`。当我们显式使用 `a.requires_grad = False` 关闭 autograd 时,计算历史不再被追踪,正如我们在计算 `b2` 时所看到的。
如果你只需要临时关闭 autograd,一个更好的方法是使用 `torch.no_grad()`
tensor([[5., 5., 5.],
[5., 5., 5.]], grad_fn=<AddBackward0>)
tensor([[5., 5., 5.],
[5., 5., 5.]])
tensor([[6., 6., 6.],
[6., 6., 6.]], grad_fn=<MulBackward0>)
`torch.no_grad()` 也可以用作函数或方法装饰器
tensor([[5., 5., 5.],
[5., 5., 5.]], grad_fn=<AddBackward0>)
tensor([[5., 5., 5.],
[5., 5., 5.]])
有一个相应的上下文管理器 `torch.enable_grad()`,用于在 autograd 未启用时将其启用。它也可以用作装饰器。
最后,你可能有一个需要梯度追踪的张量,但你想要一个不需要它的副本。为此,我们有 `Tensor` 对象的 `detach()` 方法 - 它创建一个张量的副本,该副本*从*计算历史中分离出来
tensor([0.9486, 0.8612, 0.2239, 0.8685, 0.9611], requires_grad=True)
tensor([0.9486, 0.8612, 0.2239, 0.8685, 0.9611])
我们上面这样做是因为我们想绘制一些张量。这是因为 `matplotlib` 需要 NumPy 数组作为输入,而 PyTorch 张量到 NumPy 数组的隐式转换对于 `requires_grad=True` 的张量不启用。制作一个分离的副本可以让我们继续前进。
Autograd 和就地操作#
在本笔记本中的所有示例中,我们都使用了变量来捕获计算的中间值。Autograd 需要这些中间值来执行梯度计算。*因此,在使用 autograd 时,你必须小心使用就地操作。* 这样做会破坏你在 `backward()` 调用中计算导数所需的信息。PyTorch 甚至会阻止你尝试对需要 autograd 的叶子变量进行就地操作,如下所示。
注意
以下代码单元格将引发运行时错误。这是预料之中的。
a = torch.linspace(0., 2. * math.pi, steps=25, requires_grad=True)
torch.sin_(a)
Autograd Profiler#
Autograd 会详细追踪你计算的每一步。这样的计算历史,加上时间信息,将成为一个有用的分析器 - 而 autograd 具有内置的此功能。这是一个简单的用法示例
device = torch.device('cpu')
run_on_gpu = False
if torch.cuda.is_available():
device = torch.device('cuda')
run_on_gpu = True
x = torch.randn(2, 3, requires_grad=True)
y = torch.rand(2, 3, requires_grad=True)
z = torch.ones(2, 3, requires_grad=True)
with torch.autograd.profiler.profile(use_cuda=run_on_gpu) as prf:
for _ in range(1000):
z = (z / x) * y
print(prf.key_averages().table(sort_by='self_cpu_time_total'))
/var/lib/workspace/beginner_source/introyt/autogradyt_tutorial.py:485: FutureWarning:
The attribute `use_cuda` will be deprecated soon, please use ``use_device = 'cuda'`` instead.
------------------------------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------
Name Self CPU % Self CPU CPU total % CPU total CPU time avg Self CUDA Self CUDA % CUDA total CUDA time avg # of Calls
------------------------------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------
cudaEventRecord 43.09% 8.380ms 43.09% 8.380ms 2.095us 0.000us 0.00% 0.000us 0.000us 4000
aten::div 23.90% 4.649ms 23.90% 4.649ms 4.649us 8.455ms 50.02% 8.455ms 8.455us 1000
aten::mul 23.66% 4.601ms 23.66% 4.601ms 4.601us 8.448ms 49.98% 8.448ms 8.448us 1000
cudaGetDeviceProperties_v2 9.24% 1.797ms 9.24% 1.797ms 1.797ms 0.000us 0.00% 0.000us 0.000us 1
cudaDeviceSynchronize 0.09% 17.910us 0.09% 17.910us 17.910us 0.000us 0.00% 0.000us 0.000us 1
cudaDeviceGetStreamPriorityRange 0.01% 2.880us 0.01% 2.880us 2.880us 0.000us 0.00% 0.000us 0.000us 1
cudaStreamIsCapturing 0.01% 2.300us 0.01% 2.300us 0.767us 0.000us 0.00% 0.000us 0.000us 3
cudaGetDeviceCount 0.00% 0.380us 0.00% 0.380us 0.190us 0.000us 0.00% 0.000us 0.000us 2
------------------------------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------ ------------
Self CPU time total: 19.450ms
Self CUDA time total: 16.903ms
分析器还可以标记代码的各个子块,按输入张量形状分解数据,并将数据导出为 Chrome 跟踪工具文件。有关 API 的完整详细信息,请参阅*文档*。
高级主题:更多 Autograd 细节和高级 API#
如果你有一个具有 n 维输入和 m 维输出的函数 \(\vec{y}=f(\vec{x})\),那么完整的梯度是一个关于每个输入的所有输出的导数的矩阵,称为*雅可比矩阵*:
如果你有一个第二个函数,\(l=g\left(\vec{y}\right)\),它接受 m 维输入(即,与上述输出相同的维度),并返回一个标量输出,你可以将其关于 \(\vec{y}\) 的梯度表示为一个列向量,\(v=\left(\begin{array}{ccc}\frac{\partial l}{\partial y_{1}} & \cdots & \frac{\partial l}{\partial y_{m}}\end{array}\right)^{T}\) - 这实际上只是一个单列的雅可比矩阵。
更具体地说,将第一个函数想象成你的 PyTorch 模型(可能有很多输入和很多输出),将第二个函数想象成一个损失函数(以模型输出为输入,以损失值为标量输出)。
如果我们乘以第一个函数的雅可比矩阵和第二个函数的梯度,并应用链式法则,我们会得到
注意:你也可以使用等效操作 \(v^{T}\cdot J\),得到一个行向量。
所得的列向量是*第二个函数关于第一个函数输入的梯度* - 或者在我们的模型和损失函数的情况下,是损失关于模型输入的梯度。
``torch.autograd`` 是计算这些乘积的引擎。这就是我们在反向传播过程中累积学习权重的梯度的方式。
因此,`backward()` 调用*也可以*接受一个可选的向量输入。这个向量代表张量上的一组梯度,这些梯度被乘以其前面的 autograd 追踪张量的雅可比矩阵。让我们用一个小向量进行一个具体的例子
x = torch.randn(3, requires_grad=True)
y = x * 2
while y.data.norm() < 1000:
y = y * 2
print(y)
tensor([-1154.6906, -812.0412, 11.2324], grad_fn=<MulBackward0>)
如果我们现在尝试调用 `y.backward()`,我们会收到一个运行时错误,并提示梯度只能*隐式*地为标量输出计算。对于多维输出,autograd 期望我们提供它可以乘以雅可比矩阵的三个输出的梯度
v = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float) # stand-in for gradients
y.backward(v)
print(x.grad)
tensor([5.1200e+01, 5.1200e+02, 5.1200e-02])
(请注意,输出梯度都与二次幂有关 - 这是我们从重复加倍操作中期望的。)
高级 API#
autograd 上有一个 API,可以让你直接访问重要的微分矩阵和向量运算。特别是,它允许你计算特定函数在特定输入下的雅可比矩阵和*海森矩阵*。(海森矩阵类似于雅可比矩阵,但表示所有*二阶*偏导数。)它还提供了将向量与这些矩阵相乘的方法。
让我们计算一个简单函数在 2 个单元素输入下的雅可比矩阵,并进行求值
def exp_adder(x, y):
return 2 * x.exp() + 3 * y
inputs = (torch.rand(1), torch.rand(1)) # arguments for the function
print(inputs)
torch.autograd.functional.jacobian(exp_adder, inputs)
(tensor([0.8778]), tensor([0.1108]))
(tensor([[4.8110]]), tensor([[3.]]))
如果你仔细观察,第一个输出应该等于 \(2e^x\)(因为 \(e^x\) 的导数是 \(e^x\)),第二个值应该是 3。
当然,你也可以对高阶张量执行此操作
inputs = (torch.rand(3), torch.rand(3)) # arguments for the function
print(inputs)
torch.autograd.functional.jacobian(exp_adder, inputs)
(tensor([0.4431, 0.5910, 0.4504]), tensor([0.1194, 0.7245, 0.9486]))
(tensor([[3.1150, 0.0000, 0.0000],
[0.0000, 3.6115, 0.0000],
[0.0000, 0.0000, 3.1379]]), tensor([[3., 0., 0.],
[0., 3., 0.],
[0., 0., 3.]]))
假设你的函数是两次可微的,`torch.autograd.functional.hessian()` 方法的工作方式相同,但返回一个包含所有二阶导数的矩阵。
还有一个函数可以直接计算向量-雅可比矩阵乘积,如果你提供向量
def do_some_doubling(x):
y = x * 2
while y.data.norm() < 1000:
y = y * 2
return y
inputs = torch.randn(3)
my_gradients = torch.tensor([0.1, 1.0, 0.0001])
torch.autograd.functional.vjp(do_some_doubling, inputs, v=my_gradients)
(tensor([ 14.2352, 1376.1854, 264.1120]), tensor([2.0480e+02, 2.0480e+03, 2.0480e-01]))
`torch.autograd.functional.jvp()` 方法执行与 `vjp()` 相同的矩阵乘法,但操作数相反。`vhp()` 和 `hvp()` 方法对向量-海森乘积执行相同的操作。
有关更多信息,包括*功能 API*的文档中的性能说明
脚本总运行时间: (0 分钟 0.828 秒)
