beginner/understanding_leaf_vs_nonleaf_tutorial

在 Google Colab 中运行

Colab

下载 Notebook

Notebook

在 GitHub 上查看

GitHub

理解 requires_grad、retain_grad、叶子张量和非叶子张量

作者: Justin Silver

本教程使用一个简单的示例，解释了 requires_grad、retain_grad、叶子张量和非叶子张量的细微差别。

在开始之前，请确保您理解 张量及其操作方法。对 autograd 的工作原理 的基本了解也将很有用。

设置

首先，请确保已 安装 PyTorch，然后导入必要的库。

import torch
import torch.nn.functional as F

接下来，我们实例化一个简单的网络来关注梯度。这将是一个仿射层，后跟 ReLU 激活，最后是预测张量和标签张量之间的 MSE 损失。

\[\mathbf{y}_{\text{pred}} = \text{ReLU}(\mathbf{x} \mathbf{W} + \mathbf{b})\]

\[L = \text{MSE}(\mathbf{y}_{\text{pred}}, \mathbf{y})\]

请注意，参数（W 和 b）需要 requires_grad=True，以便 PyTorch 跟踪涉及这些张量的操作。我们将在未来的 部分 中更详细地讨论这一点。

# tensor setup
x = torch.ones(1, 3)                      # input with shape: (1, 3)
W = torch.ones(3, 2, requires_grad=True)  # weights with shape: (3, 2)
b = torch.ones(1, 2, requires_grad=True)  # bias with shape: (1, 2)
y = torch.ones(1, 2)                      # output with shape: (1, 2)

# forward pass
z = (x @ W) + b                           # pre-activation with shape: (1, 2)
y_pred = F.relu(z)                        # activation with shape: (1, 2)
loss = F.mse_loss(y_pred, y)              # scalar loss

叶子张量与非叶子张量

在执行正向传播后，PyTorch autograd 已构建了一个 动态计算图，如下所示。这是一个 有向无环图 (DAG)，它记录了输入张量（叶子节点）、对这些张量的所有后续操作以及中间/输出张量（非叶子节点）。该图使用微积分中的 链式法则，从图的根（输出）到叶子（输入）计算每个张量的梯度。

\[\mathbf{y} = \mathbf{f}_k\bigl(\mathbf{f}_{k-1}(\dots \mathbf{f}_1(\mathbf{x}) \dots)\bigr)\]

\[\frac{\partial \mathbf{y}}{\partial \mathbf{x}} = \frac{\partial \mathbf{f}_k}{\partial \mathbf{f}_{k-1}} \cdot \frac{\partial \mathbf{f}_{k-1}}{\partial \mathbf{f}_{k-2}} \cdot \cdots \cdot \frac{\partial \mathbf{f}_1}{\partial \mathbf{x}}\]

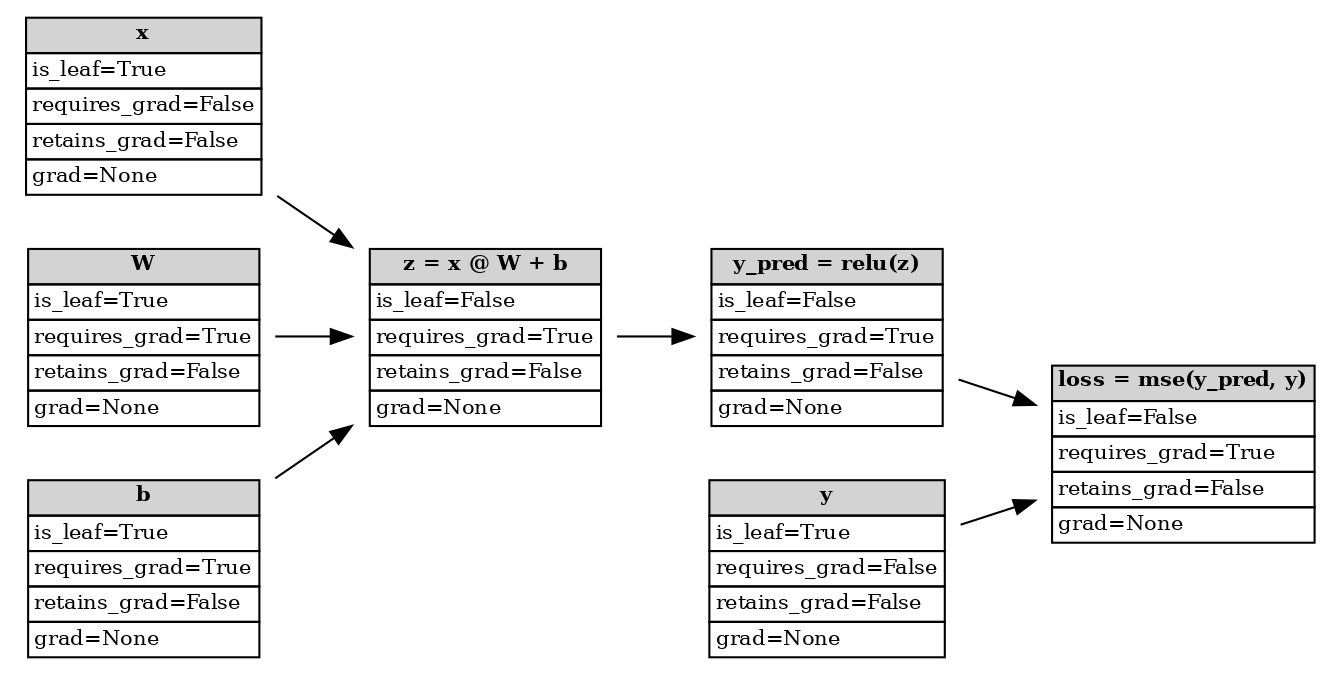
正向传播后的计算图

PyTorch 将一个节点视为叶子，如果它不是至少一个具有 requires_grad=True 的输入张量运算的结果（例如 x、W、b 和 y），而所有其他节点则被视为非叶子（例如 z、y_pred 和 loss）。您可以通过检查张量的 is_leaf 属性以编程方式验证这一点。

# prints True because new tensors are leafs by convention
print(f"{x.is_leaf=}")

# prints False because tensor is the result of an operation with at
# least one input having requires_grad=True
print(f"{z.is_leaf=}")

x.is_leaf=True
z.is_leaf=False

叶子和非叶子之间的区别决定了在反向传播后，张量的梯度是否会存储在其 grad 属性中，从而可用于 梯度下降。我们将在 下一节 中更详细地介绍这一点。

现在让我们研究一下 PyTorch 如何在其计算图中计算和存储张量的梯度。

requires_grad

为了构建可用于梯度计算的计算图，我们需要将 requires_grad=True 参数传递给张量构造函数。默认情况下，值为 False，因此 PyTorch 不会跟踪创建的任何张量的梯度。要验证这一点，请尝试不设置 requires_grad，重新运行正向传播，然后运行反向传播。您会看到

>>> loss.backward()
RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn

此错误意味着 autograd 无法反向传播到任何叶子张量，因为 loss 未跟踪梯度。如果您需要更改此属性，可以通过在张量上调用 requires_grad_() 来实现（注意后面的 _）。

我们可以像上面使用 is_leaf 属性一样，对哪些节点需要梯度计算进行健全性检查。

print(f"{x.requires_grad=}") # prints False because requires_grad=False by default
print(f"{W.requires_grad=}") # prints True because we set requires_grad=True in constructor
print(f"{z.requires_grad=}") # prints True because tensor is a non-leaf node

x.requires_grad=False
W.requires_grad=True
z.requires_grad=True

需要记住的是，非叶子张量根据定义具有 requires_grad=True，否则反向传播将失败。如果张量是叶子，那么只有当用户明确设置时，它才具有 requires_grad=True。换句话说，如果张量的至少一个输入需要梯度，那么它也会需要梯度。

此规则有两个例外：

1. 任何具有 nn.Parameter 的 nn.Module 的参数将具有 requires_grad=True（参见 此处）。

2. 使用上下文管理器本地禁用梯度计算（参见 此处）。

总之，requires_grad 告诉 autograd 需要为反向传播计算哪些张量的梯度。这不同于哪些张量的 grad 字段会被填充，这是下一节的主题。

retain_grad

为了实际执行优化（例如 SGD、Adam 等），我们需要运行反向传播以便提取梯度。

loss.backward()

backward() 调用会填充所有具有 requires_grad=True 的叶子张量的 grad 字段。 grad 是损失相对于我们正在探测的张量的梯度。在运行 backward() 之前，此属性设置为 None。

print(f"{W.grad=}")
print(f"{b.grad=}")

W.grad=tensor([[3., 3.],
        [3., 3.],
        [3., 3.]])
b.grad=tensor([[3., 3.]])

您可能想知道我们网络中的其他张量。让我们检查剩余的叶子节点。

# prints all None because requires_grad=False
print(f"{x.grad=}")
print(f"{y.grad=}")

x.grad=None
y.grad=None

这些张量的梯度未被填充，因为我们没有明确告诉 PyTorch 计算它们的梯度（requires_grad=False）。

现在让我们看一个中间非叶子节点。

print(f"{z.grad=}")

/var/lib/workspace/beginner_source/understanding_leaf_vs_nonleaf_tutorial.py:215: UserWarning:

The .grad attribute of a Tensor that is not a leaf Tensor is being accessed. Its .grad attribute won't be populated during autograd.backward(). If you indeed want the .grad field to be populated for a non-leaf Tensor, use .retain_grad() on the non-leaf Tensor. If you access the non-leaf Tensor by mistake, make sure you access the leaf Tensor instead. See github.com/pytorch/pytorch/pull/30531 for more information. (Triggered internally at /pytorch/build/aten/src/ATen/core/TensorBody.h:489.)

z.grad=None

PyTorch 返回 None 作为梯度，并警告我们正在访问非叶子节点的 grad 属性。虽然 autograd 必须计算中间梯度才能使反向传播正常工作，但它假定您之后不需要访问这些值。要更改此行为，我们可以对张量使用 retain_grad() 函数。这会告诉 autograd 引擎在调用 backward() 后填充该张量的 grad。

# we have to re-run the forward pass
z = (x @ W) + b
y_pred = F.relu(z)
loss = F.mse_loss(y_pred, y)

# tell PyTorch to store the gradients after backward()
z.retain_grad()
y_pred.retain_grad()
loss.retain_grad()

# have to zero out gradients otherwise they would accumulate
W.grad = None
b.grad = None

# backpropagation
loss.backward()

# print gradients for all tensors that have requires_grad=True
print(f"{W.grad=}")
print(f"{b.grad=}")
print(f"{z.grad=}")
print(f"{y_pred.grad=}")
print(f"{loss.grad=}")

W.grad=tensor([[3., 3.],
        [3., 3.],
        [3., 3.]])
b.grad=tensor([[3., 3.]])
z.grad=tensor([[3., 3.]])
y_pred.grad=tensor([[3., 3.]])
loss.grad=tensor(1.)

我们获得的 W.grad 结果与之前相同。另外请注意，由于损失是标量，损失相对于其自身的梯度就是 1.0。

如果我们查看计算图现在的状态，我们会发现中间张量的 retains_grad 属性已发生更改。按约定，此属性将打印 False 对于任何叶子节点，即使它需要其梯度。

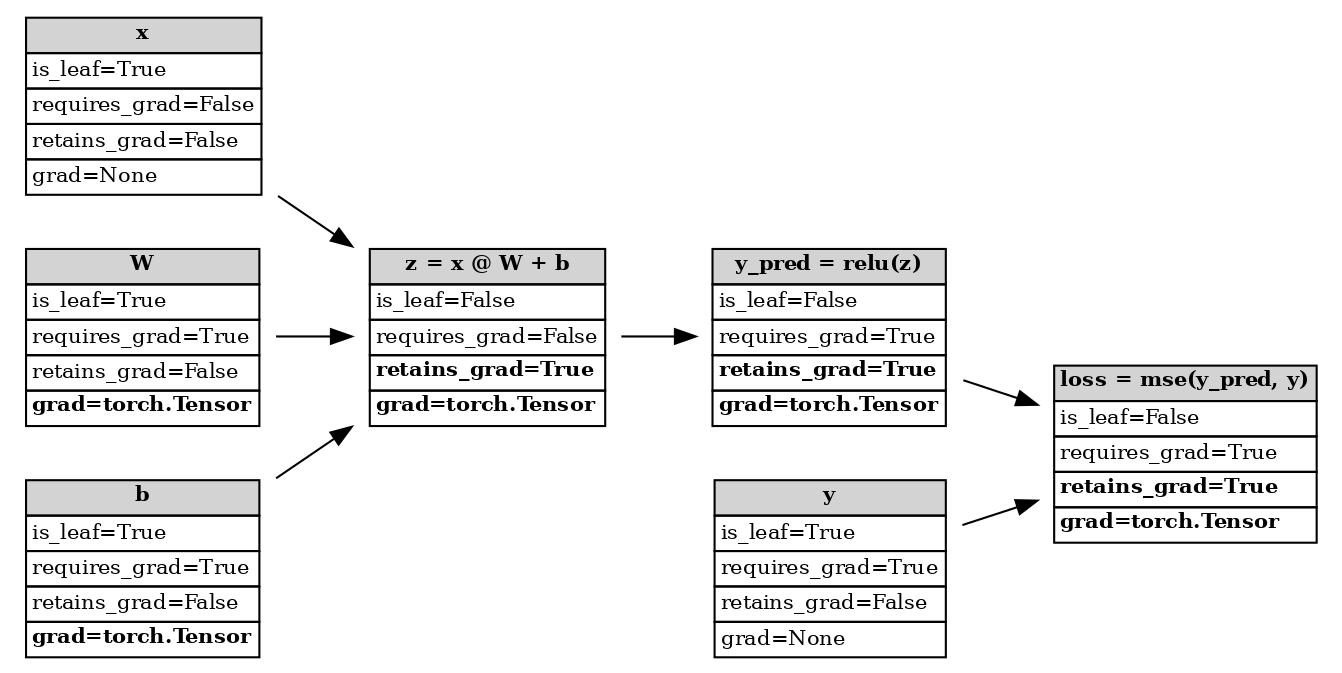
反向传播后的计算图

如果您对非叶子节点调用 retain_grad()，则不会产生任何效果。如果我们对具有 requires_grad=False 的节点调用 retain_grad()，PyTorch 实际上会抛出错误，因为它无法存储梯度（如果它从未被计算过）。

>>> x.retain_grad()
RuntimeError: can't retain_grad on Tensor that has requires_grad=False

摘要表

使用 retain_grad() 和 retains_grad 仅对非叶子节点有意义，因为对于具有 requires_grad=True 的叶子张量，grad 属性已经填充。默认情况下，这些非叶子节点在反向传播后不保留（存储）其梯度。我们可以通过重新运行正向传播，告诉 PyTorch 存储梯度，然后执行反向传播来更改此行为。

下表可用作参考，总结了上述讨论。以下场景是 PyTorch 张量唯一有效的场景。

is_leaf	requires_grad	retains_grad	require_grad()	retain_grad()
真	假	假	将 requires_grad 设置为 True 或 False	无操作
真	真	假	将 requires_grad 设置为 True 或 False	无操作
假	真	假	无操作	将 retains_grad 设置为 True
假	真	真	无操作	无操作

结论

在本教程中，我们涵盖了 PyTorch 何时以及如何为叶子和非叶子张量计算梯度。通过使用 retain_grad，我们可以访问 autograd 计算图中中间张量的梯度。

如果您想了解更多关于 PyTorch 的 autograd 系统如何工作的信息，请访问下面的 参考资料。如果您对此教程有任何反馈（改进、拼写错误修复等），请使用 PyTorch 论坛 和/或 issue 跟踪器 联系我们。

参考资料

• torch.autograd 的温和介绍

• 使用 torch.autograd 进行自动微分

• Autograd 机制