评价此页
★ ★ ★ ★ ★
torch.autograd">
beginner/basics/autogradqs_tutorial

注意

前往底部 下载完整示例代码。

学习基础知识 || 快速入门 || 张量 || 数据集 & DataLoader || Transforms || 构建模型 || 自动微分 || 优化 || 保存 & 加载模型

使用 torch.autograd 进行自动微分#

创建时间：2021年2月10日 | 最后更新：2024年1月16日 | 最后验证：2024年11月5日

在训练神经网络时，最常用的算法是反向传播。在该算法中，参数（模型权重）会根据损失函数相对于给定参数的梯度进行调整。

为了计算这些梯度，PyTorch 拥有一个内置的微分引擎，称为 torch.autograd。它支持对任何计算图进行自动梯度计算。

考虑最简单的单层神经网络，它具有输入 x、参数 w 和 b，以及某个损失函数。它可以用 PyTorch 以以下方式定义：

import torch

x = torch.ones(5)  # input tensor
y = torch.zeros(3)  # expected output
w = torch.randn(5, 3, requires_grad=True)
b = torch.randn(3, requires_grad=True)
z = torch.matmul(x, w)+b
loss = torch.nn.functional.binary_cross_entropy_with_logits(z, y)

张量、函数和计算图#

此代码定义了以下计算图：

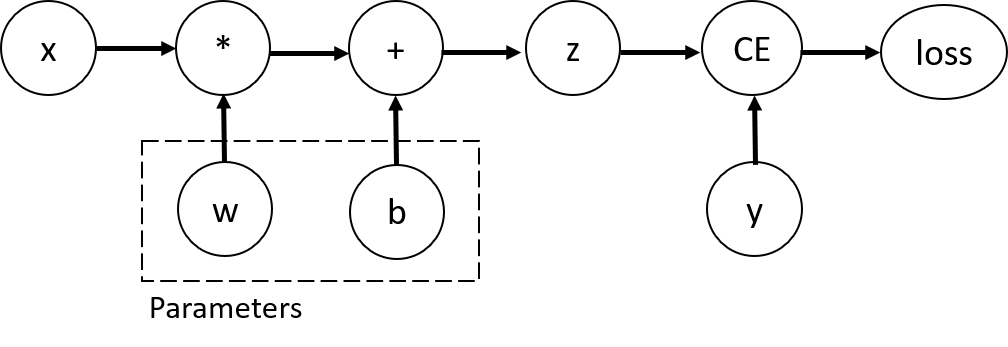
在此网络中，w 和 b 是参数，我们需要对它们进行优化。因此，我们需要能够计算损失函数相对于这些变量的梯度。为了做到这一点，我们将这些张量的 requires_grad 属性设置为 True。

注意

您可以在创建张量时设置 requires_grad 的值，或者稍后通过使用 x.requires_grad_(True) 方法来设置。

我们将用于构建计算图的函数实际上是 Function 类的一个对象。该对象知道如何在前向计算函数，也知道如何在反向传播步骤中计算其导数。反向传播函数的引用存储在张量的 grad_fn 属性中。您可以在文档中找到有关 Function 的更多信息。

print(f"Gradient function for z = {z.grad_fn}")
print(f"Gradient function for loss = {loss.grad_fn}")

Gradient function for z = <AddBackward0 object at 0x7f5e21259ff0>
Gradient function for loss = <BinaryCrossEntropyWithLogitsBackward0 object at 0x7f5e2125ad10>

计算梯度#

要优化神经网络中参数的权重，我们需要计算损失函数相对于参数的导数，即，在 x 和 y 的某些固定值下，我们需要得到 \(\frac{\partial loss}{\partial w}\) 和 \(\frac{\partial loss}{\partial b}\)。为了计算这些导数，我们调用 loss.backward()，然后从 w.grad 和 b.grad 中检索值。

loss.backward()
print(w.grad)
print(b.grad)

tensor([[0.0082, 0.2994, 0.0587],
        [0.0082, 0.2994, 0.0587],
        [0.0082, 0.2994, 0.0587],
        [0.0082, 0.2994, 0.0587],
        [0.0082, 0.2994, 0.0587]])
tensor([0.0082, 0.2994, 0.0587])

注意

  • 我们只能获取计算图叶子节点（其 requires_grad 属性设置为 True）的 grad 属性。对于我们图中的所有其他节点，梯度将不可用。

  • 出于性能原因，我们只能对给定的图执行一次梯度计算（调用 backward）。如果我们需要在同一图上进行多次 backward 调用，我们需要将 retain_graph=True 传递给 backward 调用。

禁用梯度跟踪#

默认情况下，所有 requires_grad=True 的张量都会跟踪它们的计算历史并支持梯度计算。但是，在某些情况下我们不需要这样做，例如，当我们训练好模型并只想将其应用于某些输入数据时，即我们只想通过网络进行前向计算。我们可以将计算代码用 torch.no_grad() 块包围来停止跟踪计算。

z = torch.matmul(x, w)+b
print(z.requires_grad)

with torch.no_grad():
    z = torch.matmul(x, w)+b
print(z.requires_grad)

True
False

另一种实现相同结果的方法是使用张量的 detach() 方法。

z = torch.matmul(x, w)+b
z_det = z.detach()
print(z_det.requires_grad)

False
有理由禁用梯度跟踪：

  • 将神经网络中的某些参数标记为冻结参数。

  • 在只进行前向传播时加速计算，因为对不跟踪梯度的张量进行计算会更有效。

关于计算图的更多信息#

从概念上讲，autograd 在一个由 Function 对象组成的有向无环图 (DAG) 中，会记录数据（张量）和所有执行的操作（以及由此产生的新张量）。在这个 DAG 中，叶子是输入张量，根是输出张量。通过从根到叶追踪这个图，您可以使用链式法则自动计算梯度。

在前向传播中，autograd 同时执行两项操作：

  • 运行请求的操作以计算结果张量

  • 在 DAG 中维护该操作的梯度函数。

当在 DAG 根上调用 .backward() 时，反向传播开始。此时，autograd 会

  • 从每个 .grad_fn 计算梯度，

  • 将它们累积到相应张量的 .grad 属性中，

  • 使用链式法则，一直传播到叶子张量。

注意

PyTorch 中的 DAG 是动态的 一个重要的注意事项是图是从头开始重新创建的；每次调用 .backward() 后，autograd 都会开始填充一个新图。这正是允许您在模型中使用控制流语句的原因；您可以根据需要更改每个迭代的形状、大小和操作。

可选阅读：张量梯度和雅可比乘积#

在许多情况下，我们有一个标量损失函数，我们需要计算相对于某些参数的梯度。然而，在某些情况下，输出函数是一个任意张量。在这种情况下，PyTorch 允许您计算所谓的雅可比乘积，而不是实际的梯度。

对于向量函数 \(\vec{y}=f(\vec{x})\)，其中 \(\vec{x}=\langle x_1,\dots,x_n\rangle\) 和 \(\vec{y}=\langle y_1,\dots,y_m\rangle\)，\(\vec{y}\) 相对于 \(\vec{x}\) 的梯度由雅可比矩阵给出：

\[J=\left(\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{1}}{\partial x_{n}}\\ \vdots & \ddots & \vdots\\ \frac{\partial y_{m}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right)\]

PyTorch 允许您为给定的输入向量 \(v=(v_1 \dots v_m)\) 计算雅可比乘积 \(v^T\cdot J\)，而不是计算雅可比矩阵本身。这是通过将 \(v\) 作为参数传递给 backward 来实现的。 \(v\) 的大小应与我们想要计算乘积的原始张量的大小相同。

inp = torch.eye(4, 5, requires_grad=True)
out = (inp+1).pow(2).t()
out.backward(torch.ones_like(out), retain_graph=True)
print(f"First call\n{inp.grad}")
out.backward(torch.ones_like(out), retain_graph=True)
print(f"\nSecond call\n{inp.grad}")
inp.grad.zero_()
out.backward(torch.ones_like(out), retain_graph=True)
print(f"\nCall after zeroing gradients\n{inp.grad}")

First call
tensor([[4., 2., 2., 2., 2.],
        [2., 4., 2., 2., 2.],
        [2., 2., 4., 2., 2.],
        [2., 2., 2., 4., 2.]])

Second call
tensor([[8., 4., 4., 4., 4.],
        [4., 8., 4., 4., 4.],
        [4., 4., 8., 4., 4.],
        [4., 4., 4., 8., 4.]])

Call after zeroing gradients
tensor([[4., 2., 2., 2., 2.],
        [2., 4., 2., 2., 2.],
        [2., 2., 4., 2., 2.],
        [2., 2., 2., 4., 2.]])

请注意，当我们使用相同的参数第二次调用 backward 时，梯度值是不同的。发生这种情况是因为在进行 backward 传播时，PyTorch 会累积梯度，也就是说，计算出的梯度值会被加到计算图所有叶子节点的 grad 属性上。如果您想计算正确的梯度，您需要先将 grad 属性归零。在实际训练中，优化器会帮助我们做到这一点。

注意

之前我们调用了不带参数的 backward() 函数。这本质上等同于调用 backward(torch.tensor(1.0))，这在神经网络训练等标量值函数的情况下，是计算梯度的有用方法。

进一步阅读#

脚本总运行时间： (0 分钟 0.146 秒)

在此页面上
PyTorch 库